√ 平行四辺形 対角線 面積 191662

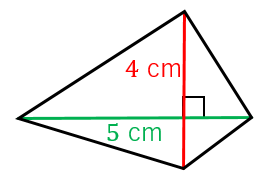
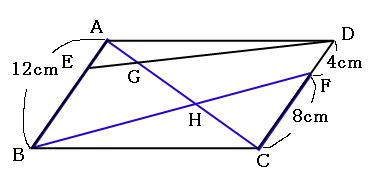
ひし形の面積 平行四辺形の面積（底辺と高さから） 平行四辺形の面積（2辺と夾角から） 円に内接する四角形の面積（4辺から） 四角形の面積（4辺と対角の和から） 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の 平行四辺形abcdがあり、対角線bdを1：2にわける点がe、bdの中点がfとなっています。 このとき、 abeと cdfの面積比を求めなさい。 この問題を解く上で、4つ目の型をおぼえてもらいた平行四辺形の面積は，次の公式で求められます。 平行四辺形の面積＝底辺×高さ 〔例〕 右の平行四辺形A日CDの面積， 辺BCを底辺とすると，直線EFが 高さになるから， 6×4＝24 で，24c㎡であることがわかる。 trsF2tmpjtd

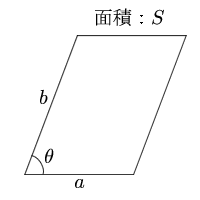
平行四辺形 2辺と間の角度 面積の計算 計算サイト

平行四辺形 対角線 面積

平行四辺形 対角線 面積-平行四辺形を二等分するためには 対角線の交点を通るように直線をひけば良かったですね。 ということで まずは、平行四辺形の対角線の交点の座標を求めます。小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題

1

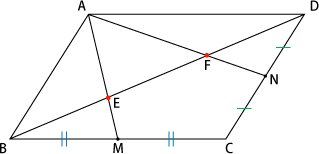
De//bcより平行線の同位角は等しいので∠aed=∠ecf ab//efより平行線の同位角は等しいので∠ead=∠cef よって2組の角がそれぞれ等しいので ade∽ efc 相似な三角形の対応する辺の比は等しいので adef=aeec 四角形dbfeは平行四辺形なので ef=db ひし形の面積 は、 対角線×もう一方の対角線÷2 で求められます。 ひし形は 横の対角線を横の辺、縦の対角線の半分を縦の辺とした長方形に変えられる からです。ひし形を対角線で4つに切ってみると分かります。 ひし形は平行四辺形の1つです。平行四辺形の性質 ③2組の向かい合う角はそれぞれ等しい ④対角線は互いに他を2等分する 10 三角形の辺と平行線 11 中点連結定理

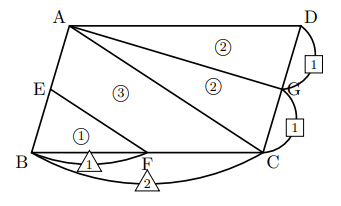
上図のように平行四辺形abcdがあります。 線分adとCBは平行四辺形の対角線です。 今、線分cd上に点Eを3：1にとり、線分beを引きました。 この時、 (三角形①の面積) ： (三角形②の面積) ： (三角形③の面積) の比を求めて下さい。長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交するひし形の面積が『対角線×対角線÷2』となる理由 考え方としては\(2\)つあります。 理由1対角線を底辺とした平行四辺形に変形できる ひし形を変形することで、一方の対角線を底辺とする平行四辺形にすることができます。

 ミズキ この平行四辺形の底辺は何センチかな？ カイト 上の辺と下の辺をくっつけてるんだから、それを足し合わせればいいんだろ？ ミズキ そうすると、底辺は6㎝2㎝で8㎝。 ミズキ それじゃ、カイちゃん、黄色の台形の面積は？ カイト 黄色の台形の面積 平行四辺形の性質を理解しているか。特に、関数の問題においては、 平行四辺形は向かい合う線分は平行なので、 「傾き」が同じ である。 平行四辺形の面積を2等分する直線は、必ず「 対角線の交点 」を通る。 目次 平行線と三角形の面積 等積変形の作図 ①四角形から三角形を作る ②折れ線を直線にする ③五角形から三角形を作る 等積変形の利用① (平行四辺形の中の三角形) 等積変形の利用② (面積を求める) 平行線と面積 (等積変形)のまとめ

子どもを混乱させる相似な三角形の２つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生

平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方

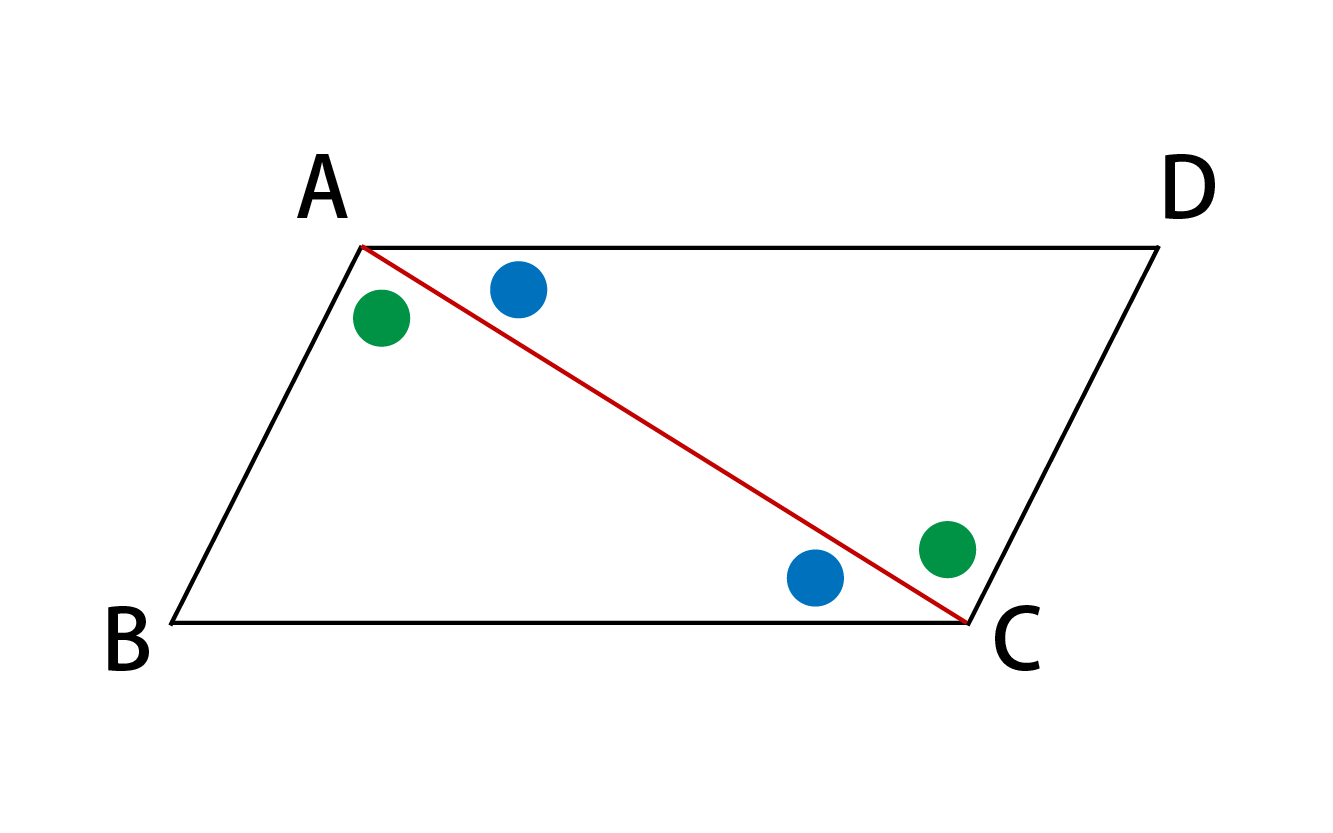
5年算数「平行四辺形と三角形の面積」 四角形を対角線で三角形に分 第7時(9時間取り扱い） 割するイメージがつかめる！ 本時の授業の概要 四角形を対角線によって三角形に分割して面積を求める方法を知り、三角形で分 なんとすれば、 （1）平行四辺形の二つの対角線は中点で交わるから、 一辺が等しい。 （2）対頂角は等しい （3）錯角が等しい よって、（1）～（3）より、一辺とその両端の角がそれぞれ 等しいので合同である。 したがって、黄緑色の三角形の面積は(1) 平行四辺形の対辺は平行で、長さが等しい。 B(5,4)からA(1,9)までの移動はx方向に4, y方向に5である。 C(11,3)からDも同じ移動なので 114=7, 35=8 よってD(7,8) (2) 平行四辺形の面積を2等分する直線は対角線の中点を通る。

塾 学校 家庭を結ぶ 受験情報サイト 学びネット

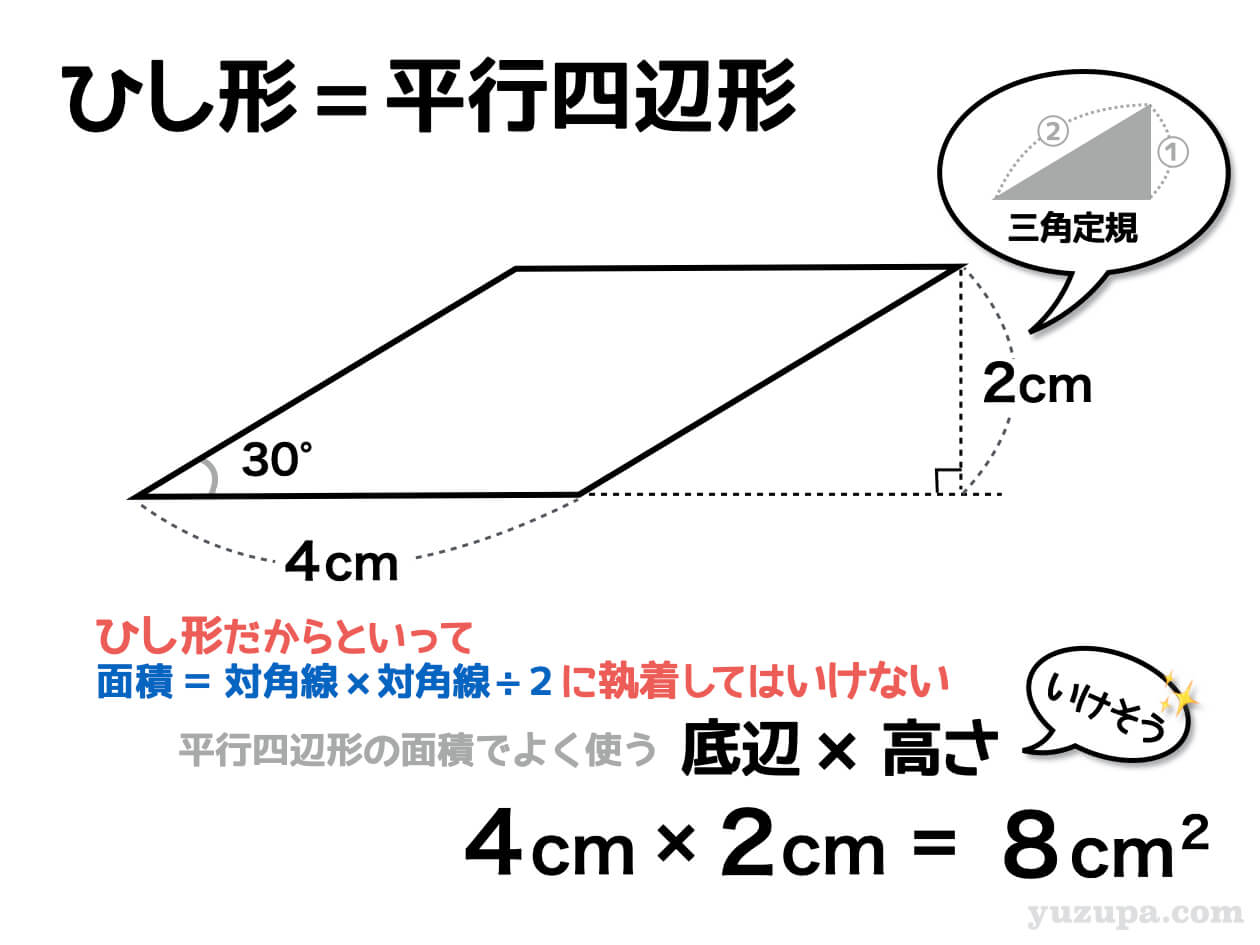
中学受験 ひし形の面積の求め方 ひとつの公式にとらわれるな かるび勉強部屋

ひし形の面積 平行四辺形の面積（底辺と高さから） 平行四辺形の面積（2辺と夾角から） 円に内接する四角形の面積（4辺から） 四角形の面積（4辺と対角の和から） 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度 これは、平行四辺形の右端の直角三角形を切り取って左側に移すと 「たて \(3cm\) 横 \(4cm\) の長方形」になるので \(たて×横=3×4=12cm^2\) からも求められますね。 ③ ひし形の面積 ひし形の面積は、\(「面積=たての対角線×横の対角線÷2」\) で求められます。

平行四辺形の対角線はそれぞれの中点で交わることの証明 をしないとい 中学校 教えて Goo

四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

平行と面積 三角形には、「底辺と高さが等しければ、形が異なっても面積は等しい」「高さの等しい三角形の面積比は、底辺の長さに比例する」という性質があります。 等積変形 （とうせきへんけい） 図形の面積を変えずに形を変えることを 等積変形 といいます。 平行四辺形の面積は「底辺×高さ」で求められたよね？？ 菱形は平行四辺形ともいえるから、 この面積の公式も使えちゃうってわけさ。 じゃんじゃん計算していこう！！ まとめ：ひし形の面積の求め方は2通りおさえよう！ ひし形の面積の求め方は、 対角 対角線bdを引いて, bdfと bdeの和として考える。 ここで, bdf＝ adf＝ bde＝ cde＝ よって四角形ebfdの面積は (cm) 別解 平行四辺形abcdから abeと bcfを取り除いた割合を 96cm にかけて求める。 平行四辺形abcdの面積を96とすると、 abe＝ bcf＝ よって

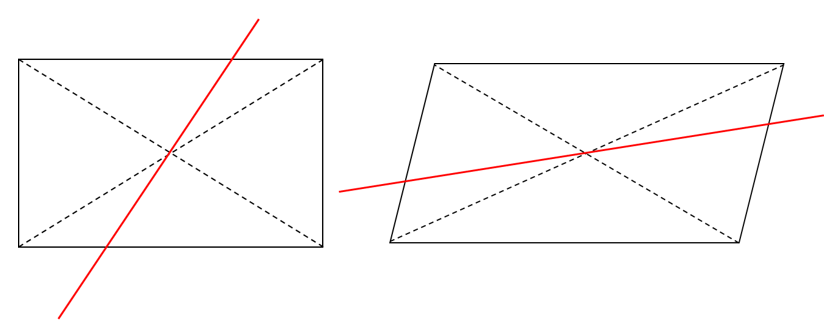
面積を2等分する考え方 中学受験プロ講師ブログ

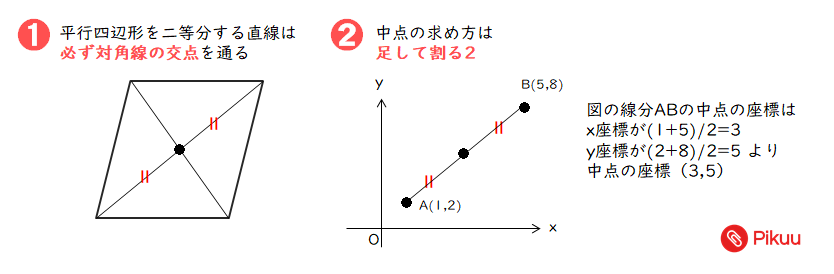
中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu

平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(l,m,n\) 31 平行四辺形の性質その1：対辺の長さが等しい 32 平行四辺形の性質その2：対角の大きさが等しい 33 平行四辺形の性質その3：対角線が他の対角線の中点を通る 4 平行四辺形の面積 (公式・証明) 5 平行四辺形の成立条件 51 平行四辺形の成立条件その1：2平行四辺形に対角線を引くと、2つの対角線が交わる点が、それぞれの対角線の中央にきます。 上記は平行四辺形の性質なので、是非理解しましょう。 平行四辺形の面積 平行四辺形の面積は、 底辺×高さ で計算します。下図のように、平行四辺形に垂直線

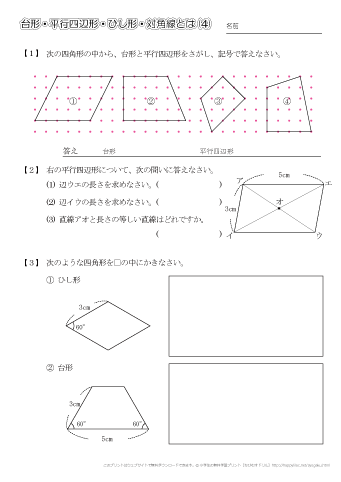
小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

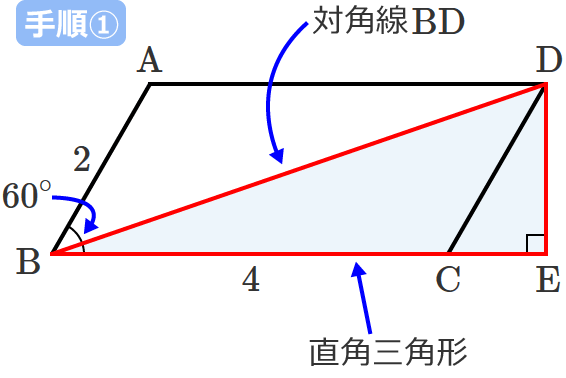
平行四辺形の対角線の長さの求め方

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators たとえば、「4辺の長さがそれぞれ 5, 15, 8, 12 で1組の対角の和が 150 ° の四角形」の面積は、ブレートシュナイダーの公式を使うことで 30 30 3 ≒ 8196 と求まります。 ただし、 ∠ A と ∠ C の角度がそれぞれ分かっている場合は、 三角形の面積の公式 を

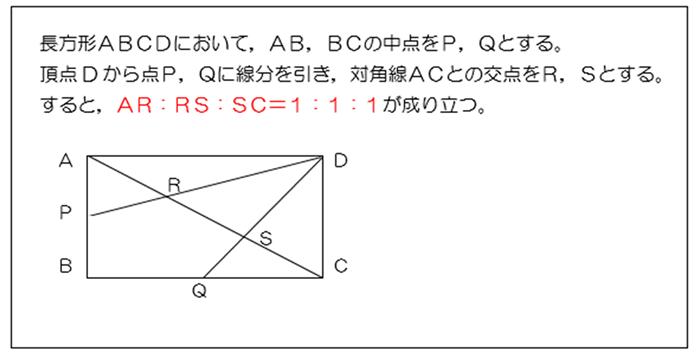
授業実践記録 数学 新しい 定理 とその活用 啓林館

平行四辺形の辺や角を求める Youtube

1

高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月

中学数学 平行四辺形の対角線 面積について 平行四辺形の対角 数学 教えて Goo

平行四辺形対角線の求め方と面積について 対角線ａｃの長さの Yahoo 知恵袋

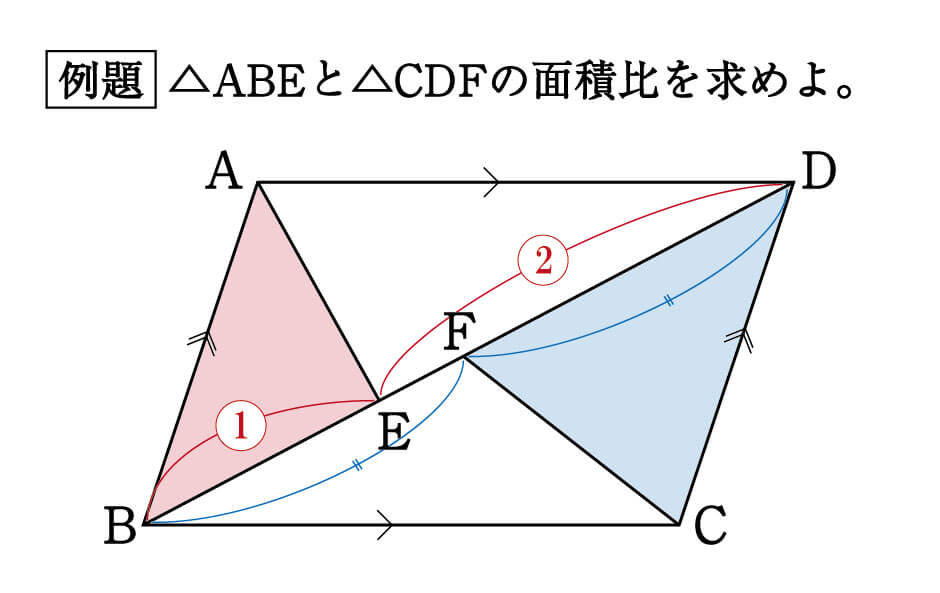
数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

Math 平行四辺形 平行四辺形になることの証明 働きアリ

1

無料 中２数学 標準問題 解答プリント 232 平行四辺形３ 長方形とひし形

平行四辺形の問題です 平行四辺形abcdがあります 辺ａｂを2 3に分 数学 教えて Goo

四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ

ひし形 の 対角線 の 長 さ

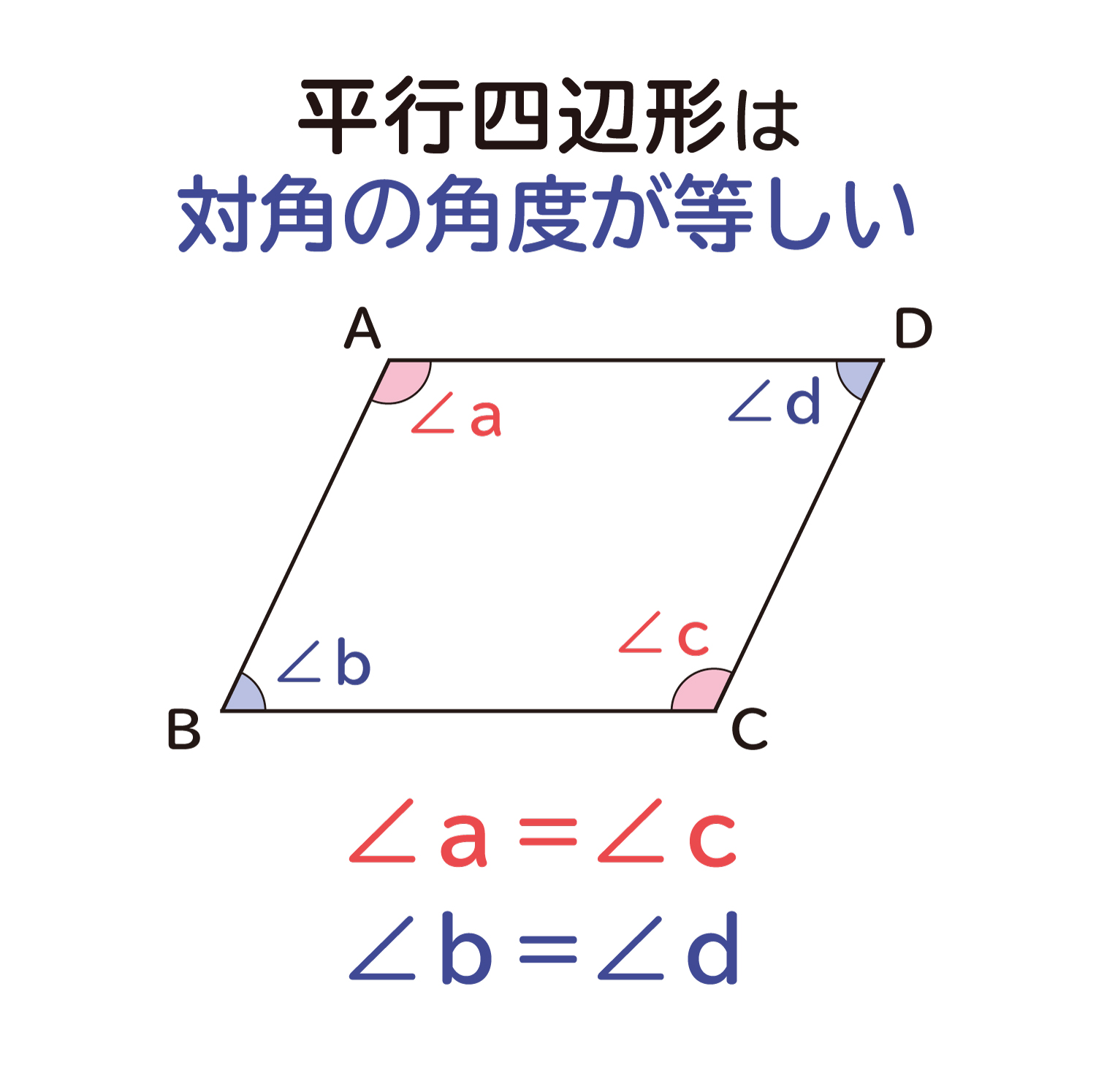
平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

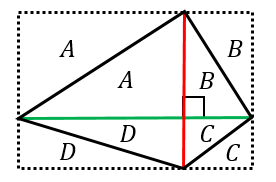
四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学

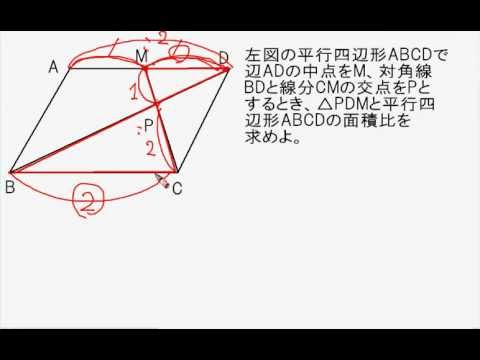
ご質問への解説 平行四辺形面積比 Youtube

５年算数三角形と四角形の面積2 教え方 台形 ひし形

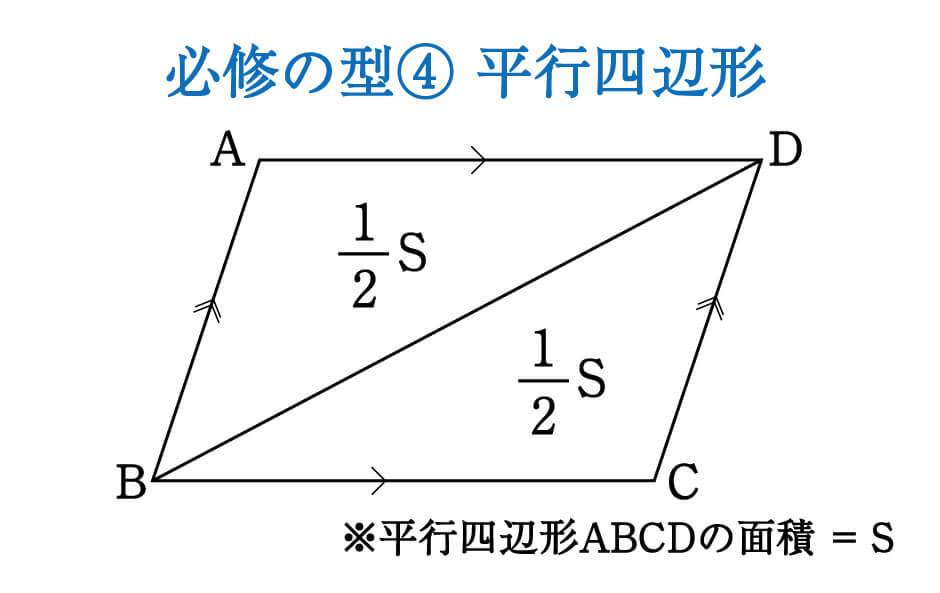
数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

2

平行四辺形の面積の２等分

平行四辺形 2辺と間の角度 面積の計算 計算サイト

ボード 勉強 のピン

平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は４つ 中学や高校の数学の計算問題

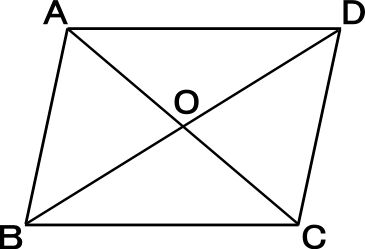
中学２年数学練習問題 平行四辺形になる条件と証明方法 図形と合同

平行 四辺 形 対角線 平行四辺形とは 定義 条件 性質や面積の公式 証明問題

攻略法 平行四辺形と面積 数樂管理人のブログ

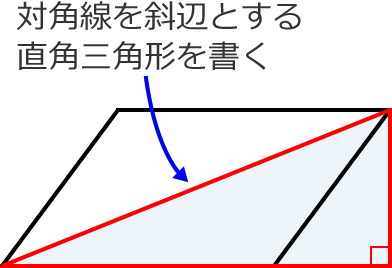
平行四辺形の対角線の長さの求め方

攻略法 平行四辺形と面積 数樂管理人のブログ

平行四辺形の対角線の交点を頂点とする三角形の面積 Okwave

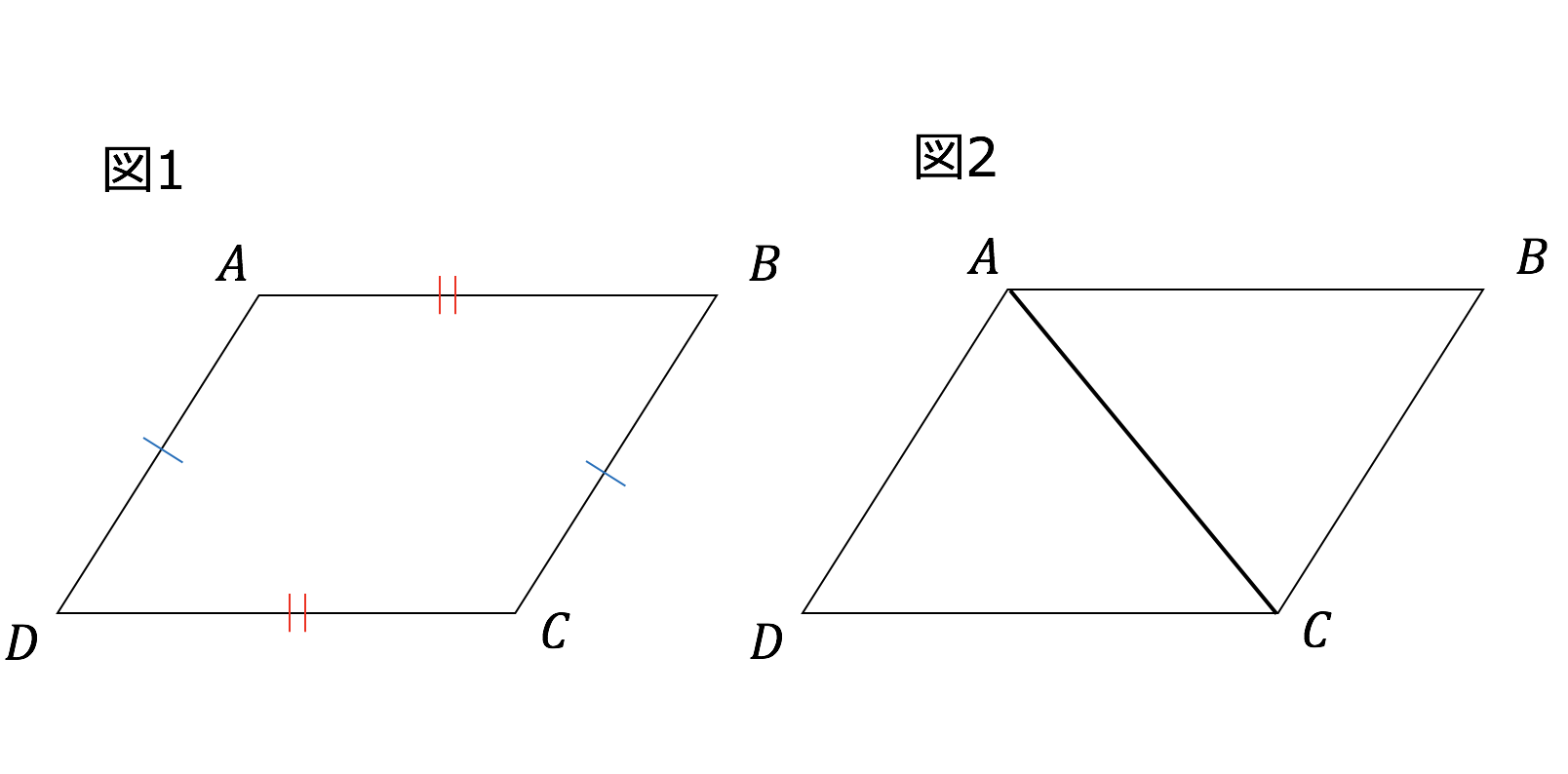
3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

三角形の面積比を解説 平面図形が苦手な人でもわかりやすい解き方 基本編 中学受験ナビ

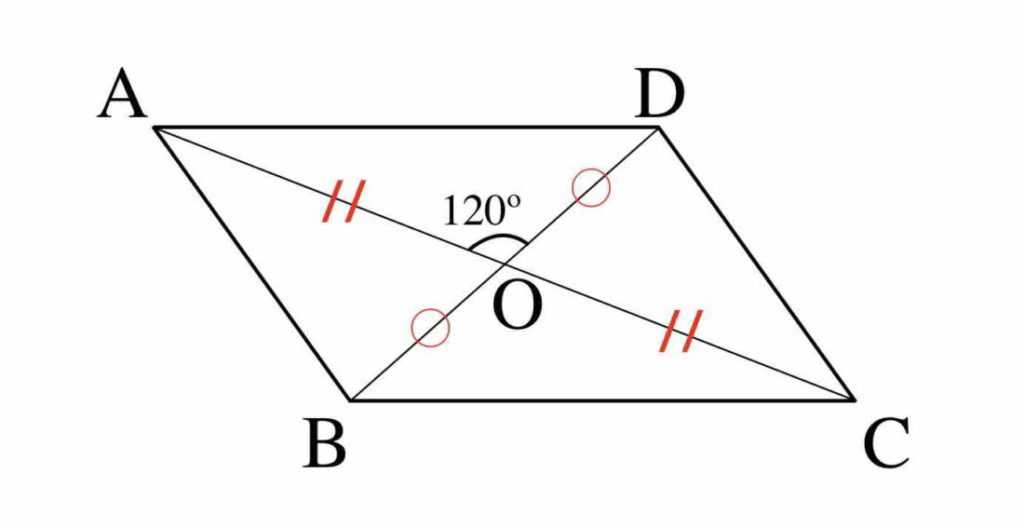
三角比を用いた面積計算をマスターしよう スタディクラブ情報局

コレクション 平行四辺形 対角線 長さ 等しい ニスヌーピー 壁紙

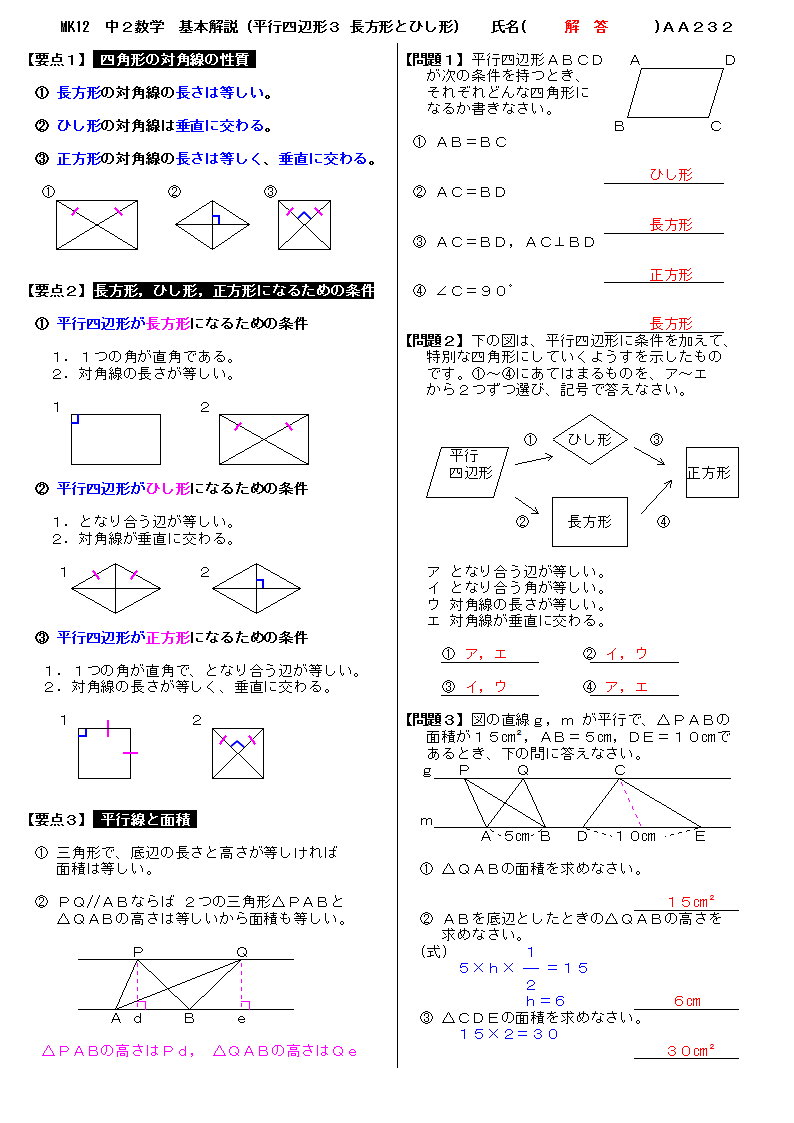
無料 中２数学 基本解説 解答プリント 232 平行四辺形３ 長方形とひし形

平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

付箋の部分の意味が分かりません 誰か教えてください Clearnote

中学数学 平行四辺形の高さの2つの求め方 Qikeru 学びを楽しくわかりやすく

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

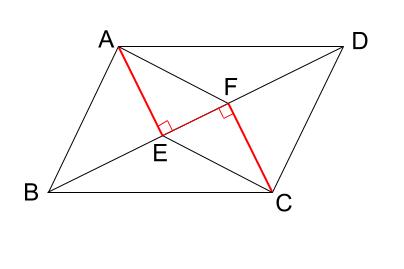
中学数学 平行四辺形になることの証明 その２ 中学数学の無料オンライン学習サイトchu Su

今月の問題 平行四辺形

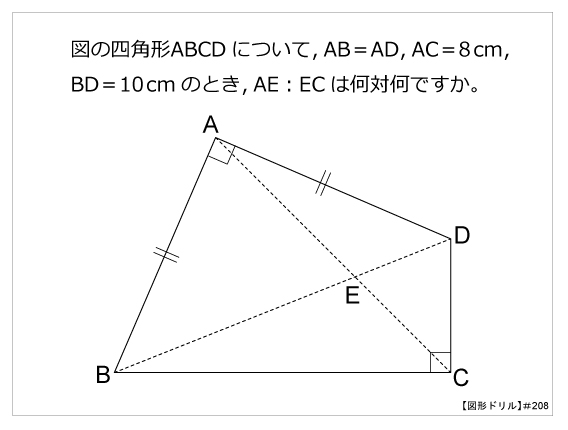
第8問 四角形の対角線 図形ドリル 第8問 四角形の対角線 算数星人のweb問題集 中学受験算数の問題に挑戦

お勉強 平行四辺形の面積 図形の面積の比を使いこなそう そらの暇つぶしch

筑波大学附属駒場中学校２００３年第１問 解答 解説

平行四辺形の対角線の長さの求め方

平行線と面積 図で 四角形abcdは平行四辺形である 点eは辺ad上 Okwave

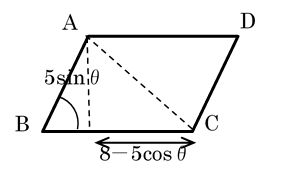
平行四辺形の面積と対角線 カワズの数学ノート 数学検定

平行四辺形を対角線で 4つにわけると 面積は4等分されますか Yahoo 知恵袋

平行四辺形の面積の２等分

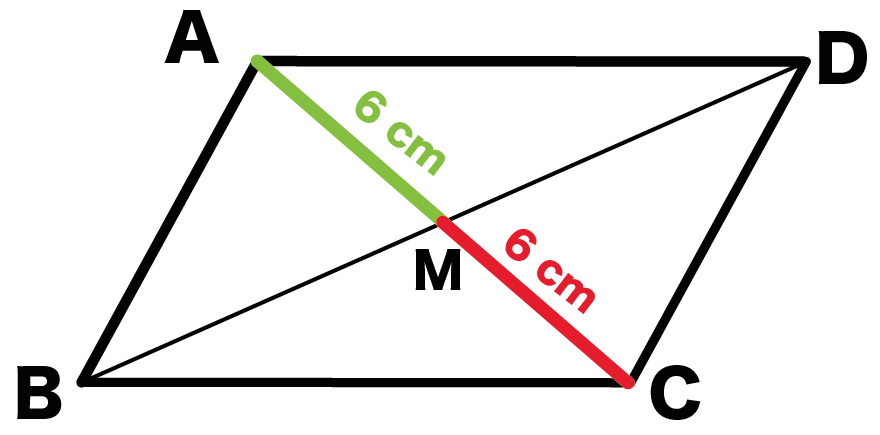
中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく

平行四辺形の対角線上の面積 Ggb Geogebra

平行線と面積

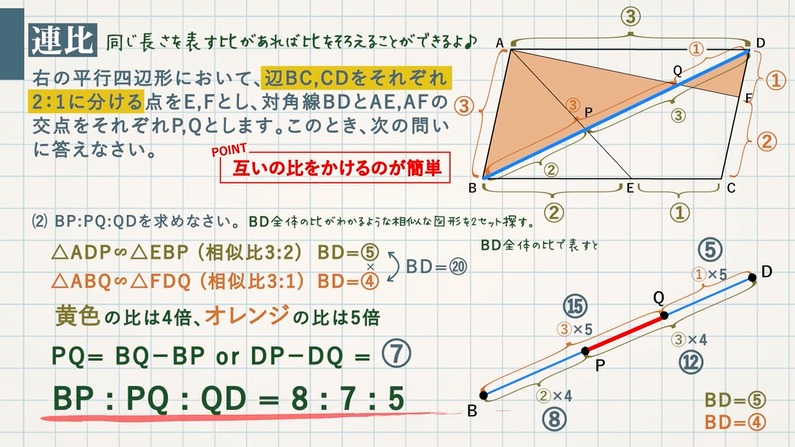
相似分野の応用問題 ラスボスっぽいの 多分それ連比です 面積の比 何倍 を求める問題も含めてかんたんな方法を解説します 教遊者

平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生

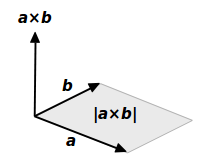
ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門

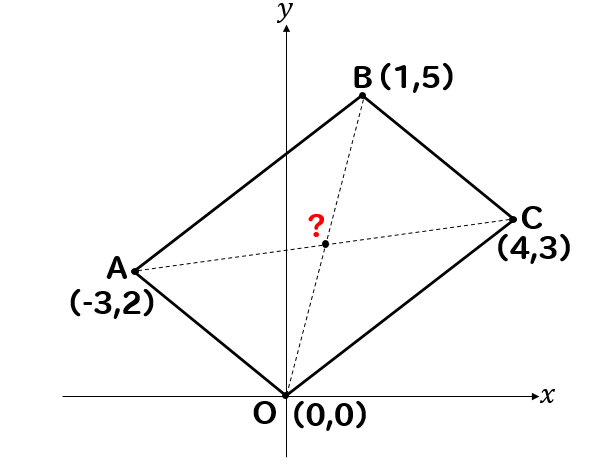
関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ

平行四辺形で知っておくべきこと 苦手な数学を簡単に

高校数学 平行四辺形の面積の求め方 例題編 映像授業のtry It トライイット

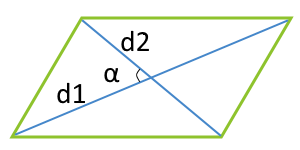
平行四辺形の面積

ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

関数13 平行四辺形の面積の二等分 Youtube

この面積比を最も簡単な整数比で表してください という問題でした わからない Clearnote

高校数学b ベクトルの成分表示と平行四辺形 受験の月

四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

平行四辺形 Wikipedia

基礎学力アップシート 3年生 平行四辺形の辺の比を考えよう

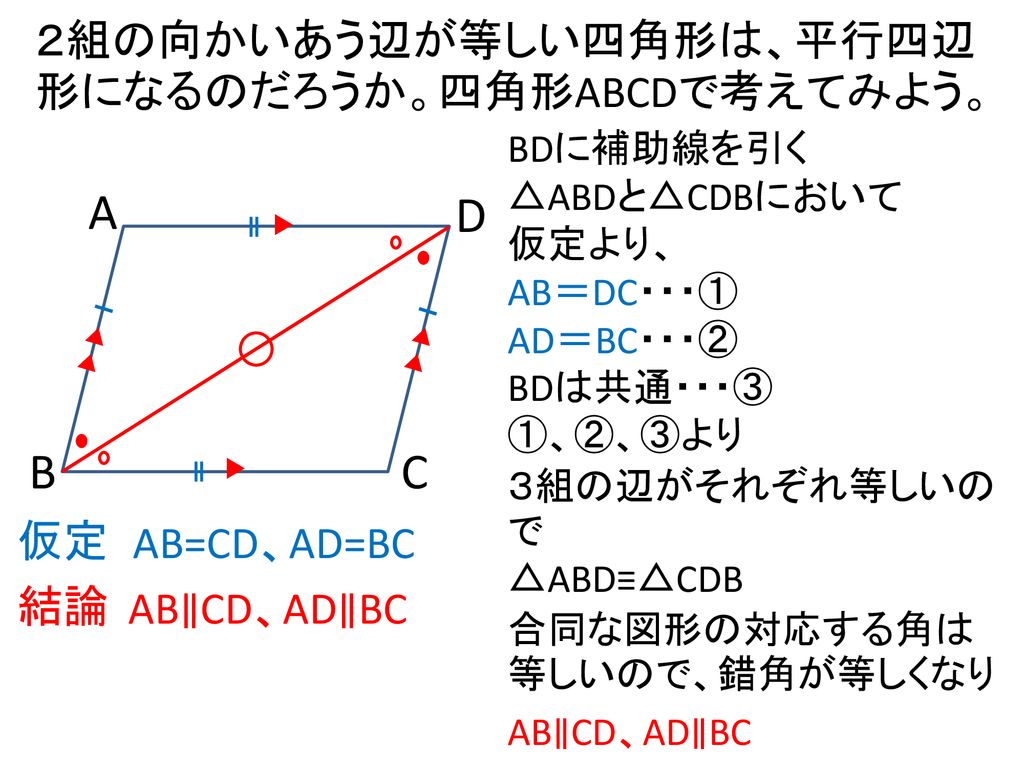
ねらい 平行四辺形の性質の逆を証明し 平行四辺形になるための条件を導くことができる Ppt Download

平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典

平行四辺形の対角線の長さの求め方

数学も英語も強くなる 意外な数学英語 Unexpected Math English Rhomboid

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

1

1

平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室

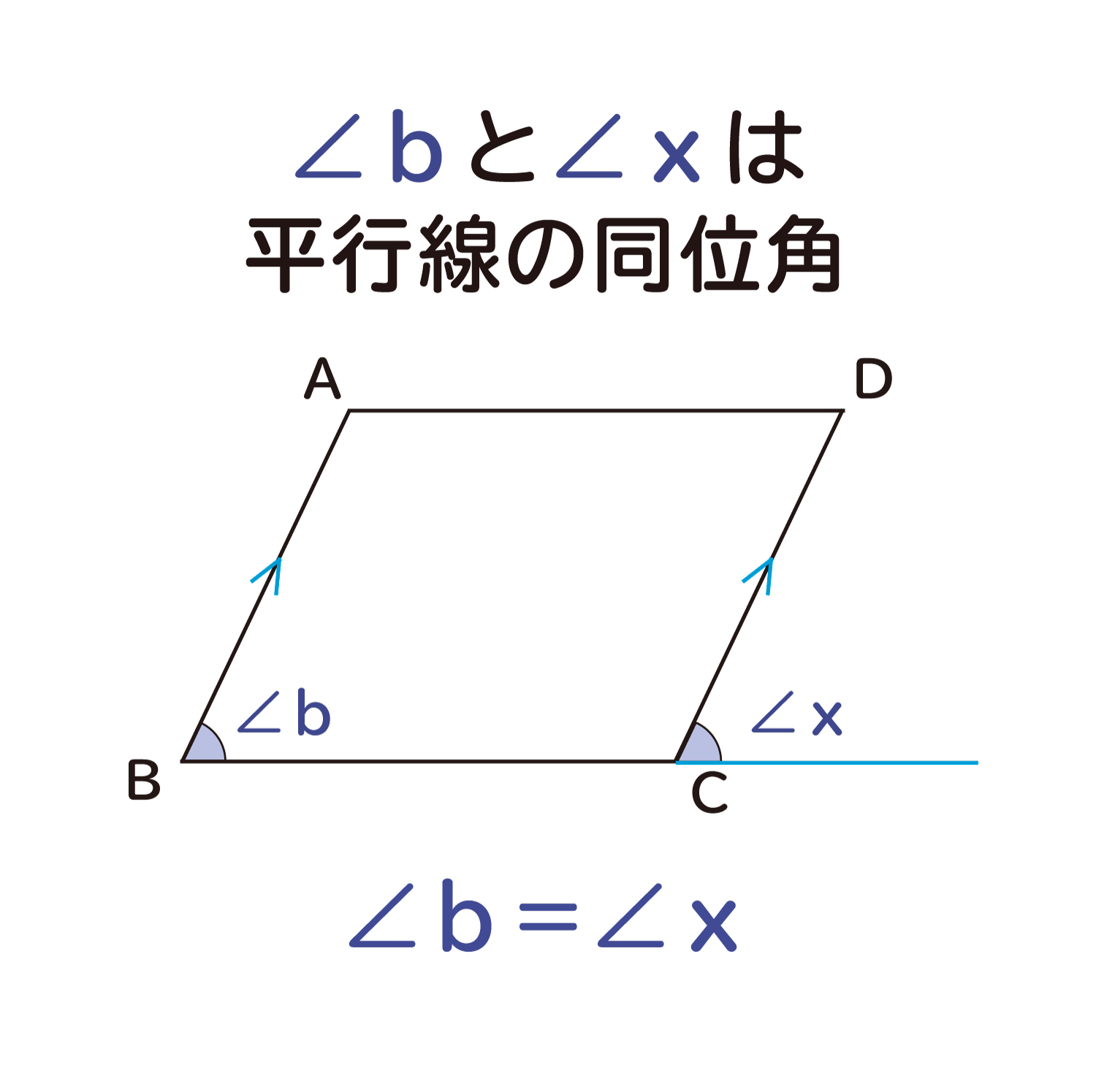
平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

平行四辺形 証明 解き方 平行四辺形 証明 解き方

平行四辺形の定義から性質と条件をわかりやすく証明 特に対角線の性質を押さえよう 遊ぶ数学

ひし形の面積の公式 面積の求め方は対角線に注目しよう 中学や高校の数学の計算問題

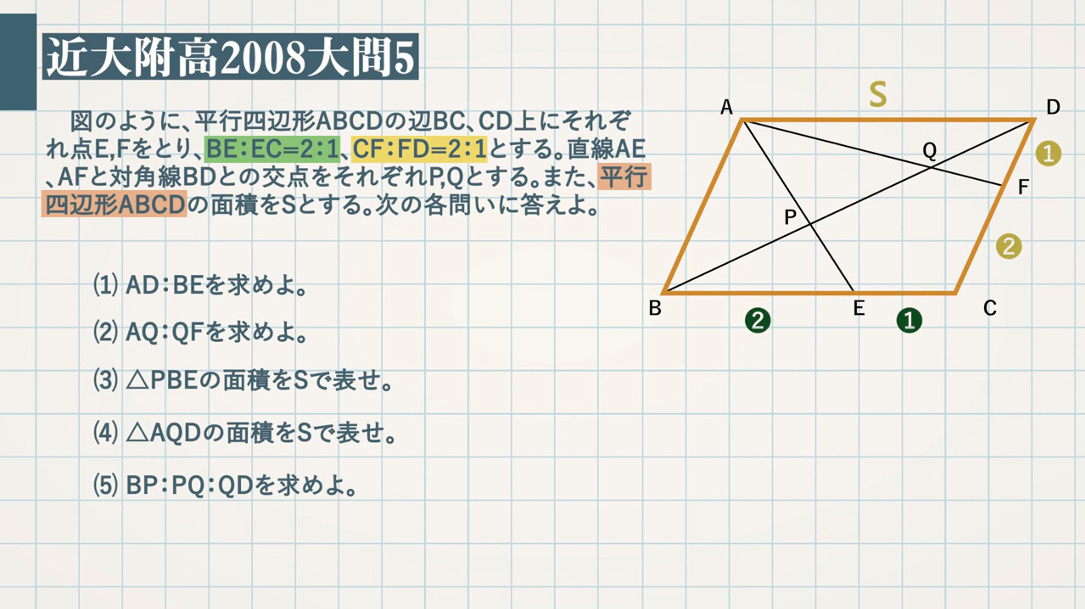
平行四辺形と比 教遊者

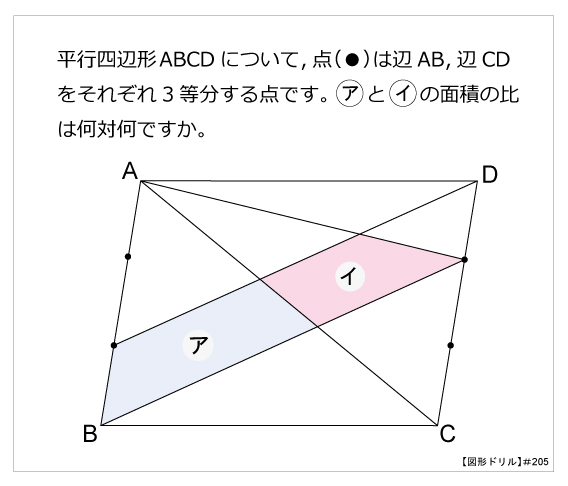
平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦

平行四辺形の対角線の中点を通る直線はその平行四辺形の面積を必ず2等分 Yahoo 知恵袋

スタディピア 図形

平行四辺形の面積の求め方 公式と計算例

図形問題が驚くほど得意になる基本問題とは あおぞら塾

小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー

平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ

相似 平行四辺形と面積比の問題を徹底解説 数スタ

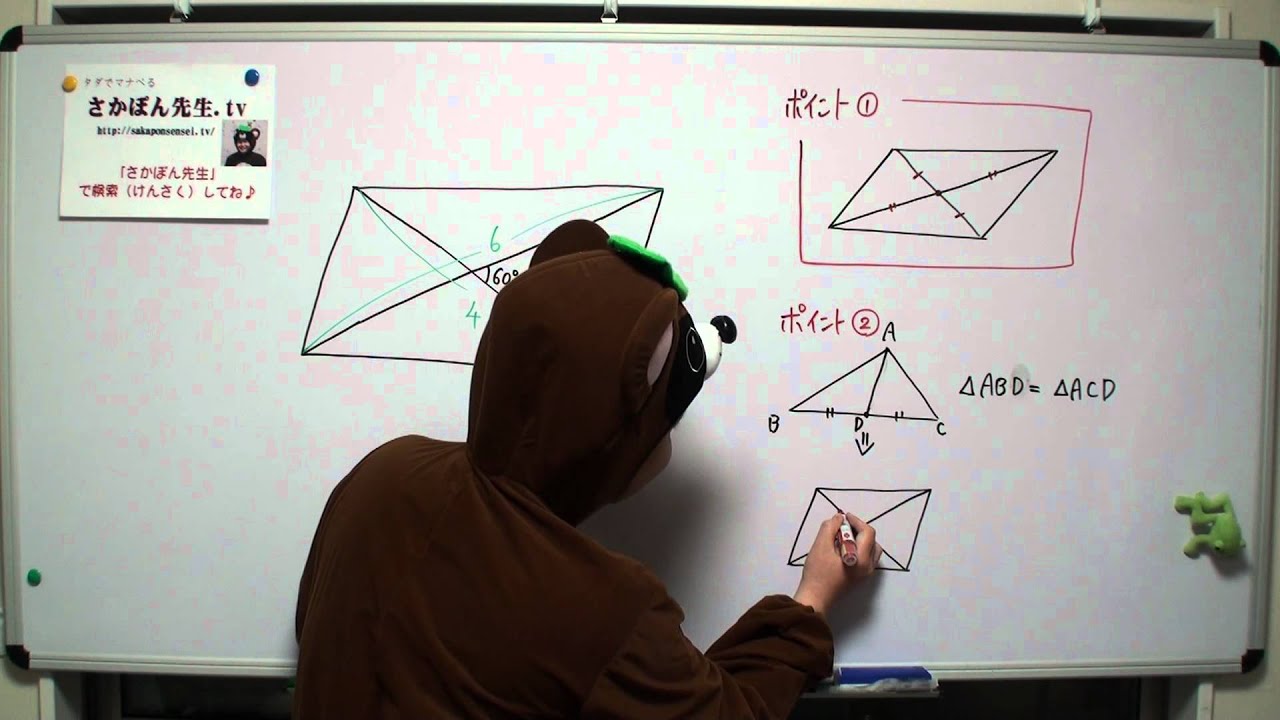
平行四辺形の面積を対角線と角度から求める問題 Youtube

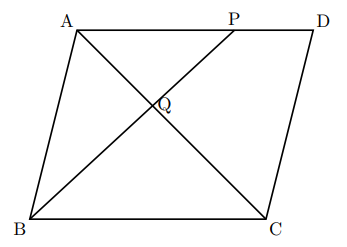
平行四辺形abcdで辺bcで中点をe ２本の対角線の交点p 対角線bdとaeの Yahoo 知恵袋

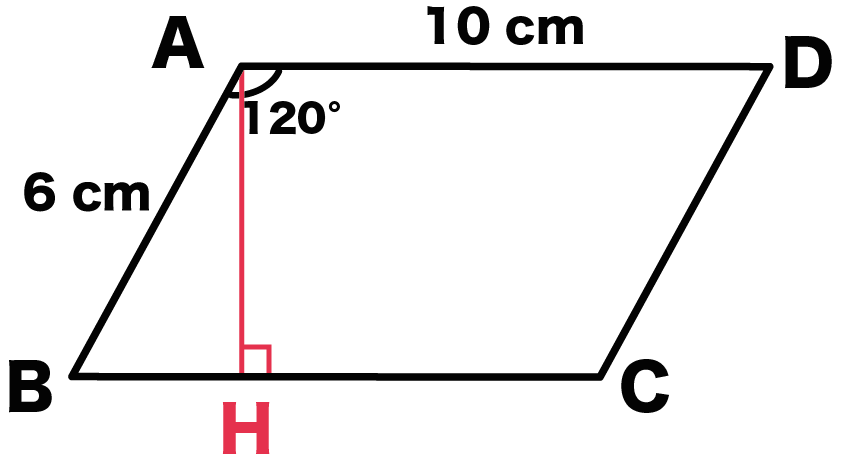
平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

平行四辺形とは 1分でわかる意味 定義 角度 面積 長方形と正方形との関係