よって、比例の式は $$\color{red}{y=2x}$$ となります。 比例の式を作りたければ、\(y=ax\)の形を覚えておいて、そこに\(x, y\)の値を代入するだけでOKですね。 比例の式グラフから式を作る 三角比を用いた代表的な計算問題をマスターしましょう。この記事では「様々な三角比の四則演算」「等式を証明するもの」「sin, cos, tan の値を計算するもの」「式の値を計算するもの」についてまとめました。本記事で取り上げた問題はどれも定期試験頻出。 となり,比の式を立てることなくACの長さを直接求めることができるようになる。 ここで $\dfrac{3}{5}$ は $\text{AC}\text{AB}$ の比の値を表すが,これは $\sin\theta$ であるから, \begin{align*} \text{AC}=\text{AB}\sin\theta \end{align*} となる。「比」や「割合」をしっかりと理解・活用している人は,三角比を

30 三角比の相互関係 式の値 の解き方を教えてください Clear
比の式とは
比の式とは-計算式(6)から求められた飽和水蒸気圧 P tot = 全圧 K = 乾湿計係数 ℃1 水蒸気圧Pwが分かっている場合、相対湿度RHは計算式(1)から計算できる、または 露点Tdは計算式(7)を用いて計算できる。 例 湿球温度Twetが385℃、乾球温度Tdryが400℃、全圧Ptotが1013hPaのと比の計算の解説 比は、その比に同じ数を掛けるか割った別の比と同じという性質を持っています。 12 = 24(左の比に2を掛けたのが右の比) 36 = 12(左の比を3で割ったのが右の比) 比の関係は分数の関係によくにています。 分数の場合も、分母と分子に同じ数を掛けるもしくは割った分数と同じです。 約分したら同じ分数になるということですね。 1 2 =




30 三角比の相互関係 式の値 の解き方を教えてください Clear
相似比が23であれば、長さがわかっているbcと求めるefも23であることがわかりますので、「23=6ef」という比の式が成り立ちます。これを解けばefの長さが9cmであることがわかります。 スポンサーリンク 相似比の問題例 四角形abcdと四角形efghは相似な図形です。相似比を求めなさい。 比例式の少し厄介な点は、 比の値 は、あくまでも 商 ( 割合 と考えても良い)を表しており、 文字そのものの値を表すわけではない ということです。 比の値が分数で表されるので、 約分されている と考えると分かりやすいかもしれません。 このままだと扱いに困るので、工夫する必要が比率の方程式とは、数(文字)の比を等式で示したものです。比率の方程式は「ab=cd ⇒ ad=bc」のように変形できます。3つの比率の方程式の解き方など、下記も勉強しましょう。 比例式とは?1分でわかる意味、問題と解き方、3つの場合、分数との関係 3つの数の比率と計算は?3分でわかる
今回は小学6年生で習う「比とその利用」について勉強します。 比の性質を使い、整数だけでなく小数や分数の比を簡単にする方法について学んでいきたいと思います。 比を簡単にする方法 比を簡単にする問題 問題① 問題② 問題③ スポンサードリンク (adsbygoogle = windowadsbygoogle )このように定義される比の等式 a b = x y あるいは分数の等式 a / b = x / y を比例式という。また、連比が等しいとは、 また、連比が等しいとは、 A 1 A 2 ⋯ A n = X 1 X 2 ⋯ X n A 1 X 1 = A 2 X 2 = ⋯ = A n X n {\displaystyle A_{1}A_{2}\cdots A_{n}=X_{1}X_{2}\cdots X_{n}\iff {A_{1} \over X_{1}}={A_{2} \over X_{2}}=\cdots ={A_{n} \over X_{n}}}比の方程式の文章問題 比は文章問題が多く出されます。 数式がすでに与えられていて計算するだけであれば、ルールを覚えてしまえば簡単です。しかし文章問題から方程式を自分で考えるのはコツが必要。ポイントを覚えてしまいましょう。 文章問題から比の方程式をつくる 例1) あるお
前年比や伸び率(増減比)の意味と求め方定義 それではまず、前年比の定義について確認していきます。 前年比とは売り上げ、利益、販売個数などの項目において、ある対象の年の数値に対する一つ前の年の数値との比といえます。 計算式としては電力比、電圧比、電流比のデシベル(dB) 電力比 の デシベル(dB) は、 電力(簡略説明) P 1 と P 2 があった場合、以下の式で求められます。 基準にしたい方を分母に持っていきます。 なお、ある電気回路において、 P 1 を入力、 P 2 を出力とした場合比例式で分数や小数のあるものや(かっこ)のついた問題の解き方です。 比例式の処理の仕方はいろいろありますが、解き方は1つなので簡単です。 ここでは整数の比だけではなく、いろいろなタイプを解いておきましょう。 この比例式は



比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support
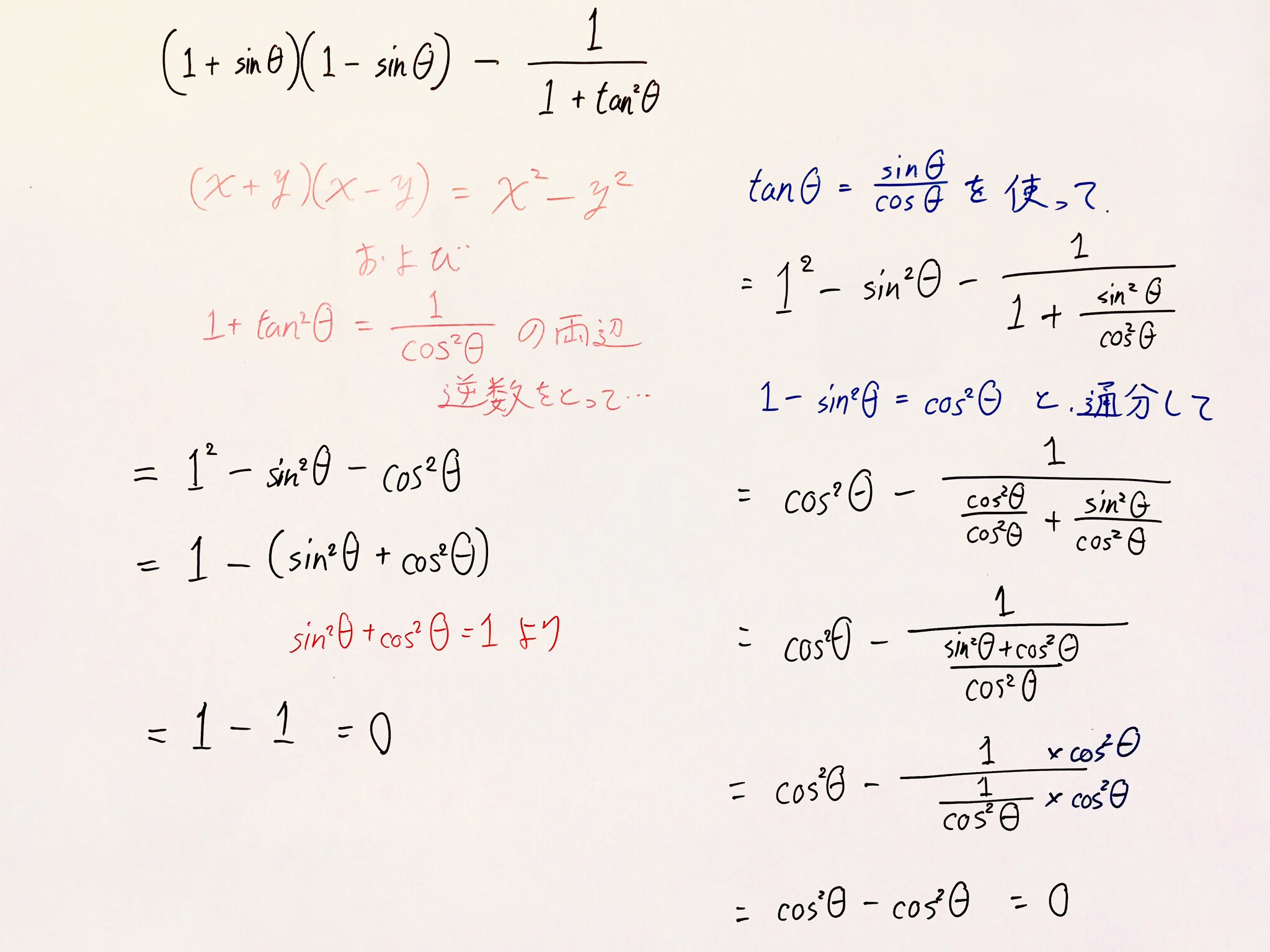



塾長 個別指導塾forward 数学ia 三角比 の計算 Tan二乗とcos二乗の公式 を使った解答と 使わない解答 使わないと変形が面倒だが できる 三角比の式は色々な崩し方があるので 模範解答にとらわれず色々な解き方を試してみよう 公式は忘れては
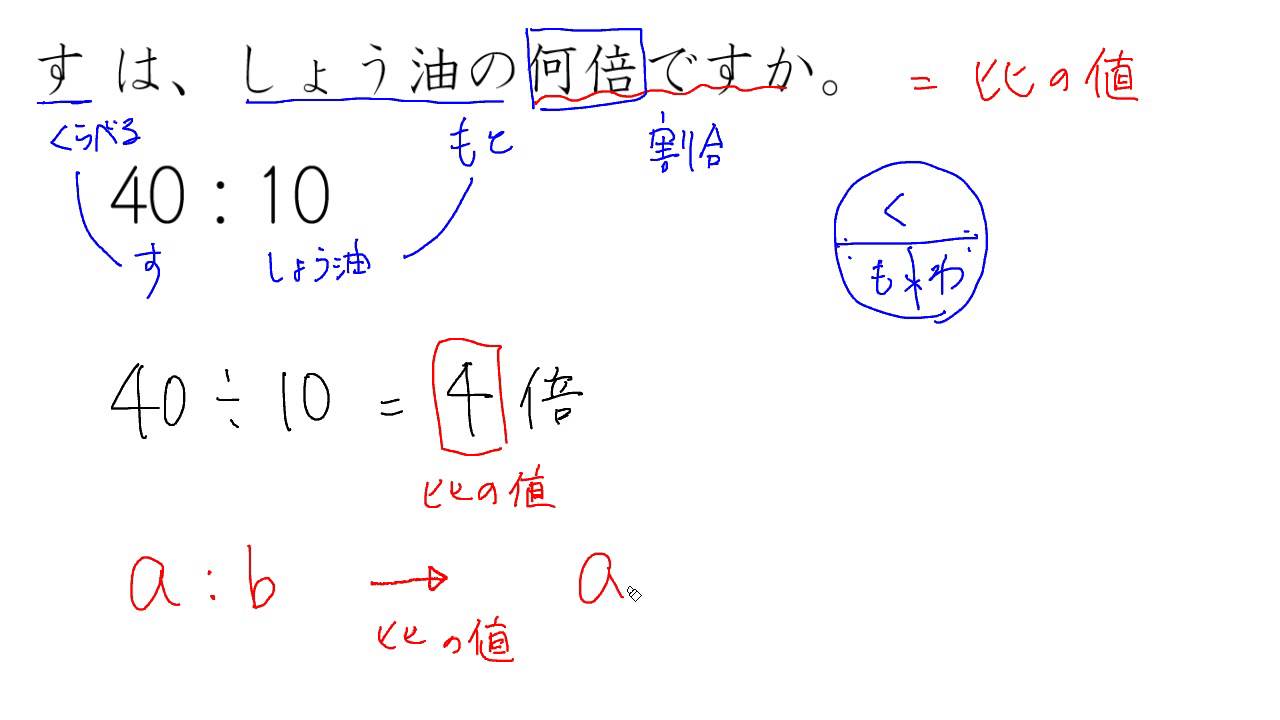
こんにちは、ウチダです。 今日は、中学1年生で習う 「比例式」 について、まず分数を用いた計算方法からある重要な公式を導き出します。 また、記事の後半では、かっこを含む比例式の計算を要する文章問題なども解説していきます。 比例式とは 比例式三角比の式の値は入試や模試などでよく見かける問題です。 和、差が与えられているときには両辺を2乗して積を求めることができる。 この考え方と式の変形について覚えておけば楽勝な問題です。 サクッと解けるように練習しておいてくださいね(/・ω・)/A:Bの比について、Bを基準にするときの割合を比の値といいます。 先ほど「A:B=3:7」の比について、Bを基準にすると$B×\displaystyle\frac {3} {7}=A$と表すことができると説明しました。 このとき、$\displaystyle\frac {3} {7}$を比の値といいます。 比の値を計算するとき、:の記号を÷に変えることで比の値をだせます。 なお、 比の値は重要ではありません。 小学算数で



2



身の回りの比
A:bの比の値は,aがbの何倍になっているかを表す数です。このことから考えても,比は割合の1つの表し方であるといえます。 なお,比と比の値を等号で結んでよいかどうかは定義によりますが,小学校では,比は2 つの数量の関係を表すことから,等号では結ばないことにしています。 ・比をSn比は、次の式で計算される。 望大特性 望大特性は、その値をできる限り無限大に近づけることが目標である。 値が大きくなるほど、理想に近づく。 特性値の逆数を望小にしている形である。 sn比は、次の式で計算される。 望目特性 望目特性は、非負でターゲット値を持つ特性であり比例式(ひれいしき)とは、比あるいは連比に関する等式のことである。 A に対する B の割合が、X に対する Y の割合に等しいとき、 AB=XY と書く 引用: 比例式について wikipedia 用途: 画像の比率計算や個人的なゲームのレベルアップまでの時間計算など色々使ってる。 例の式 4000=x100 0x=4000 x=4000/0
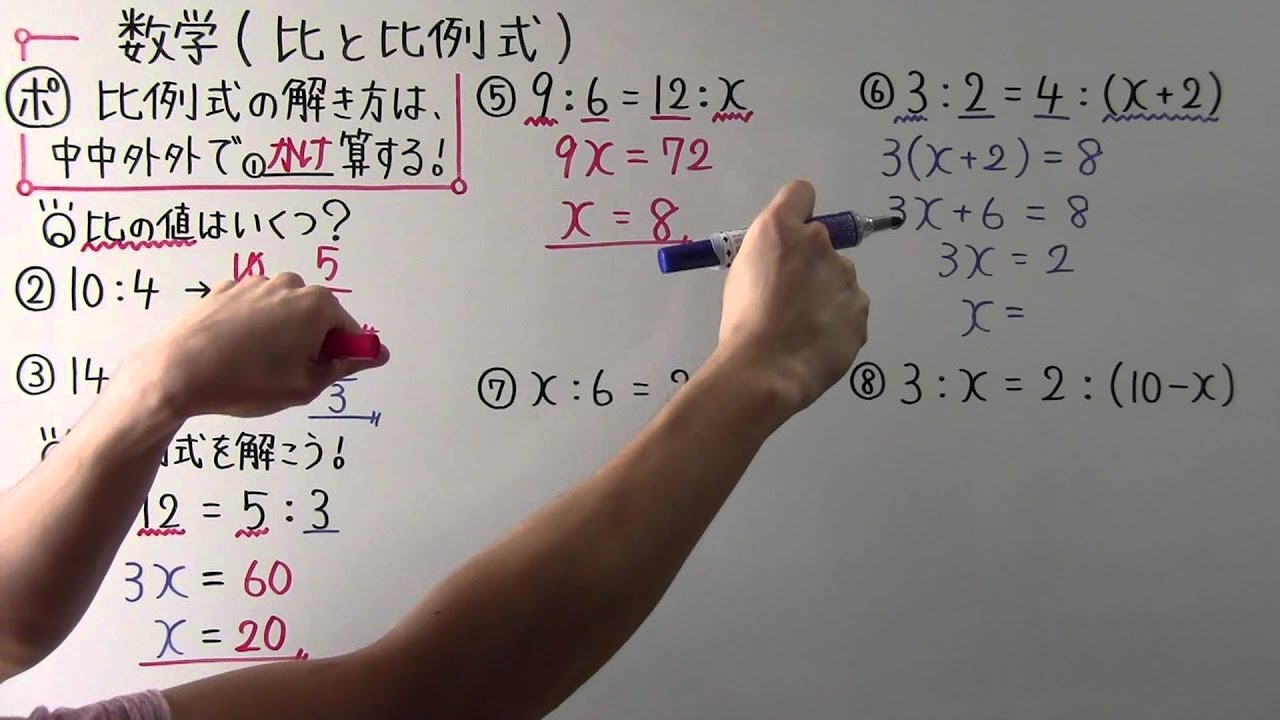



中1 数学 中1 32 比と比例式 Youtube




比率の計算
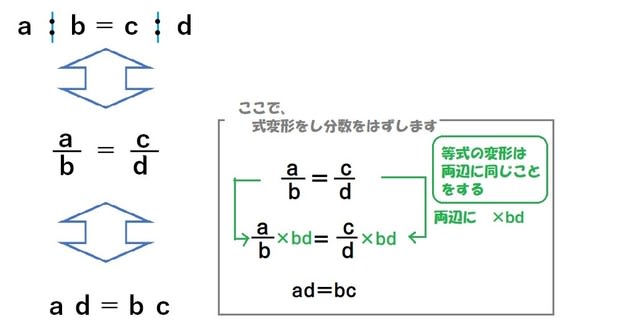
比の方程式 比の方程式は内項の積$=$外項の積で求めることができます。 $\displaystyle{AB=CD}$では、内側の$B$と$C$が内項、外側の$A$と$D$が外項です。 積とはかけ算の答えですから、「内項のかけ算」と「外項のかけ算」の答えは同じ、という意味です。比の値は a/b になります。 すると、左辺の「ab」の比の値は「a/b」、右辺の「c d」比の値は「c/d」になります。 つまり、「a b = cd」となるときは2つの比の値が等しくなり 「a/b=c/d」となることを意味します。 ab = cd ならば a/b=c/d このことから「比例式の性質」の式が得られます。 次は「比例式の性質」の式を作ってみましょう。 比や比の値が等しいことを表す等式のことを、比例式(proportionalexpression) と言います。例えば、比が等しいことを表した次の等式\ xy = 12 \や、比の値が等しいことを表した次の等式\ \frac{x}{y}=\frac{1}{2} \のような式を、比例式と呼びます。




比例式の問題 解き方のコツは この合言葉を覚えるだけ 中学や高校の数学の計算問題




数学ia 三角比を含む等式の証明 大学入試数学の考え方と解法
比の性質から「等しい比の比の値は等しい」ので、 a b = m n なら a b = m n である。 両辺に bnをかけると an = bm となる。 比例式の定義 に対する の割合が、 に対する の割合と等しいとき、 比または比の値を使って と表せる。 上記の等式を「比例式」という。 比 数量の割合を のように表したもの。 特に、 つ以上の数の比は「 連比 」という( など)。 また、, は「比の項」という。 比の値 比の後項に対する前項の割合(前項 後項の値)。 比 の比の値は 。 比例式の性質 比例式には、次の性質があります。 比エンタルピーを求める計算式で、 とある例題では、 理想空気、体積一定、密閉容器で 加温した場合のエンタルピー変化をもとめよ では Δh=m*Cv*ΔT 別の問題では 理想空気、容積一定、密閉容器で 加温した場合の比エンタルピーをもとめよ では Δh=Cp*ΔT で計算されています。




何故 の式は両辺に16をかけるのですか 自分は が4cosだから の両辺に4 Clearnote




数学 三角比の式の値を求めよ 隠れた条件を見落とすな 数スタ
返送比 とは 返送比は維持管理指標の一つとしてよく挙げられる一つです。 下水処理施設では反応タンク内のmlss 下水処理 下水三種合格講座 目次 返送比 とは2つの返送比の式は同じものなのかそれぞれの式が等しくなるという証明 返送比 とは 返送比は維持管理指標の一つとしてよく挙おわりに 広告 ※ お知らせ:東北大学21年度理学部AO入試II期数学第2問 を解く動画を公開しました。 比例式と式の値その1 例題1 $\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}$ が成り立つとき、 $\dfrac{a}{bc}$ の値を求めなさい。 標準比例式と恒等式の この2番目の考え方が「比」と言われるものです。 比の計算方法 上で説明したお小遣いの事例について、それを正確な算数のルールの中で解答するには、以下のような方法をとることになります。 太郎と花子のお小遣いの比を表すと、 0:300 となる。この式を整理すると、二つの数字の最大公約数は100であるから
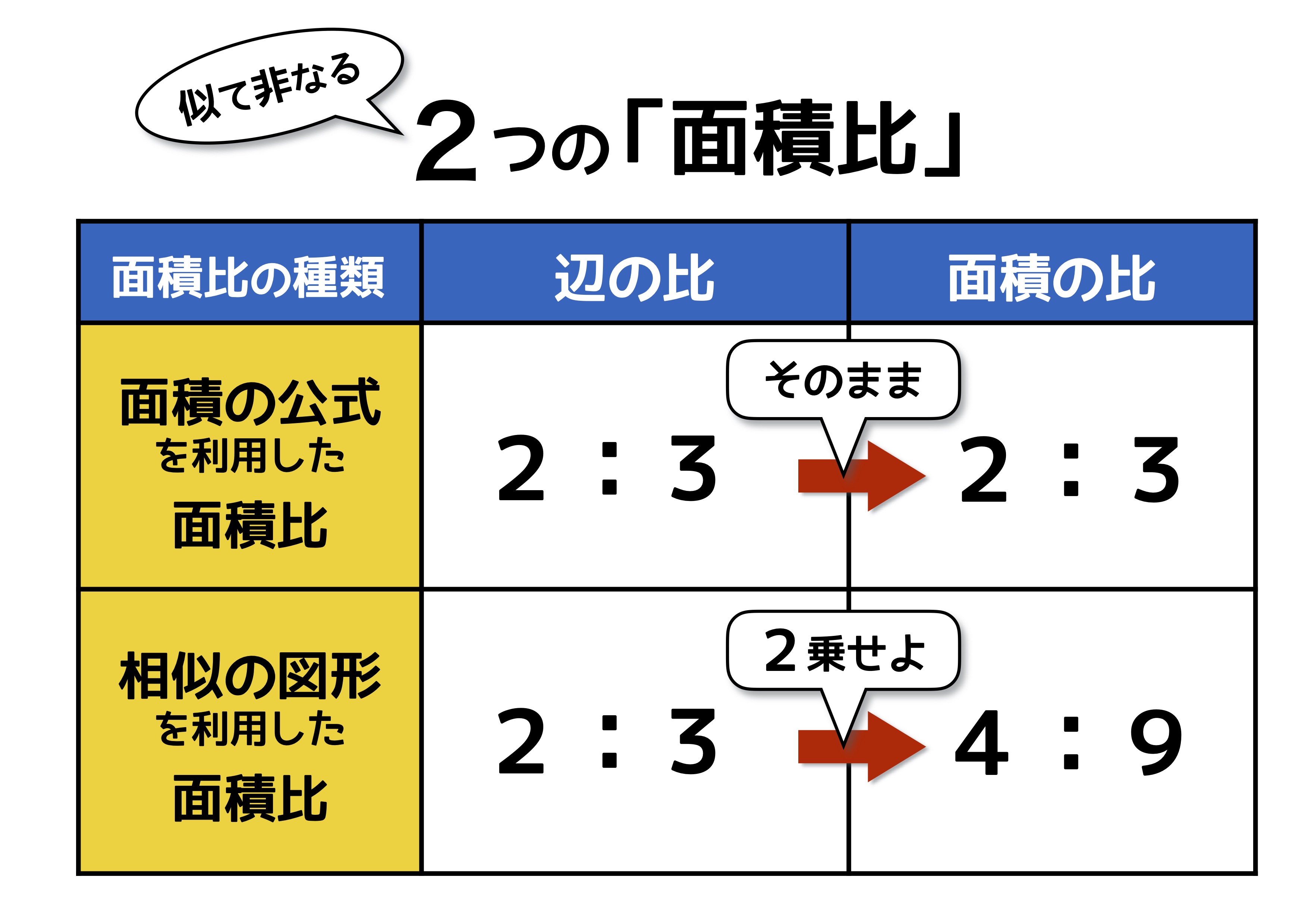



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
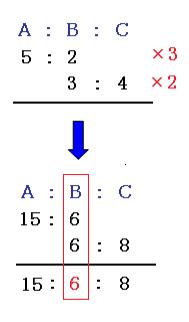



比の性質を解説 比例式や連比の解き方だってこんなに簡単
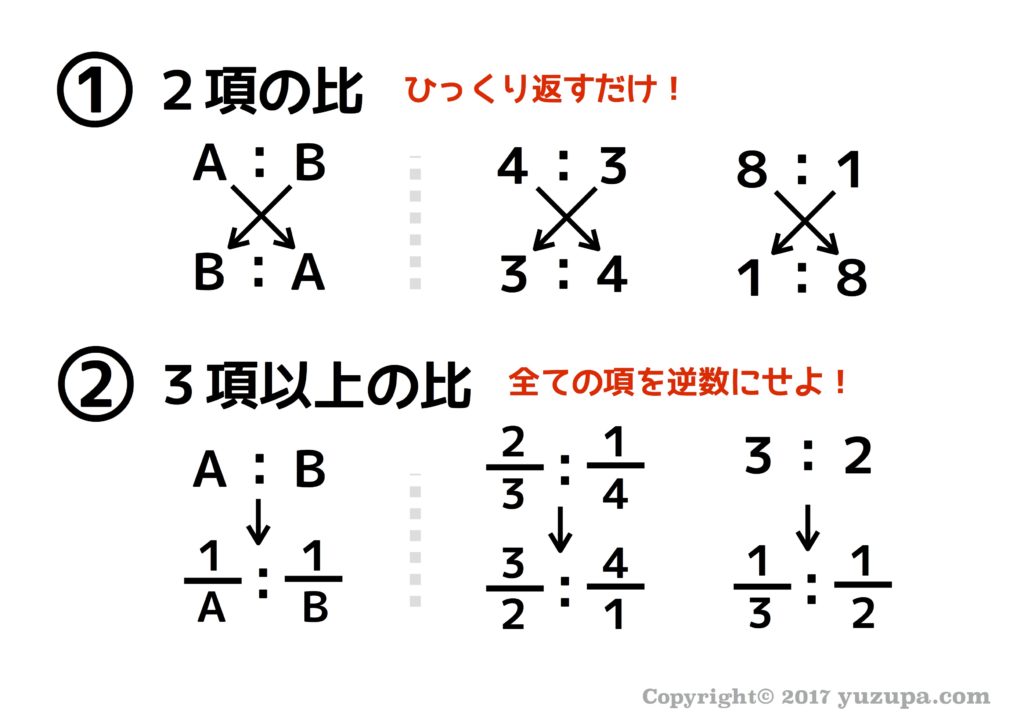
比は、同じ数をかけたり、同じ数で割ってたりしても同じ比になります。 例えば、「32」の両方を2倍して、「64」と書いても同じものです。 逆に、「164」は、どちらも4で割って「41」と書いても同じ比になります。 この性質を利用して、比はなるべく小さな整数で書くというのが決まりになっています。 例えば「2412」を、そのまま答えに書いてしまうと正解に比率の計算 計算式の入力 「農業産出額」の「構成比」を表示させましょう。表示形式はパーセント表示、小数点以下を第1位まで表示させましょう。 「構成比」とは、合計に対してそれぞれの品目の金額が占める割合のことです。 金額÷全体の合計=構成比 比を比の値にすると分数になり、分子・分母を同じ数でわったり、分子・分母に同じ数をかけることができます。 したがって、次の規則が成り立ちます。 規則 a:b=(a ÷ n):(b ÷ n)=(a × n):(b × n) 3. a:b=2:3 左辺を ab でわると、 (1/b):(1/a)=2:3 よって、(1/a):(1/b)=3:2 ・・・(答) Saturday written by 筆 者




โน ตของ 比の式 A B C Dの場合の解き方 ช น Clearnote




比の性質を解説 比例式や連比の解き方だってこんなに簡単
比の値を求めるには,比の前項を後項でわればよい。 ⑴ 12/18=12 18 =2 3 比例式の3つの項がわかっているとき,残りの項を求めることを,比例式を解 くという。内項の積と外項の積が等しいことから,方程式をつくる。比が等しいとき、その「比の値」も等しくなるので、比例式は次のように書き換えることができます。 : a b = c : d a b = c d 次に 「比の値」を整数に変える ために、 両辺に「b×d」を掛けます。 a b = c d a b × b × d = c d × b × d = a d = b c ぴよ校長 「a:b=c:d」 が 「ad=bc」 に書き換わったね! まとめ ・ 比例式「a:b=c:d」を、比の値「a/b=c/d」に書き換えます。 ・次に、 比 ABスーパーの今月の売上高は、2,000,000円でした。 肉屋は850,000円、魚屋は550,000円、米屋は600,000円でした。 その時の各構成比を計算してみます。 肉屋 = 850,000円 ÷ 2,000,000円 = 0425 (425%) 魚屋 = 550,000円 ÷ 2,000,000円 = 0275 (275%) 米屋 = 600,000円 ÷ 2,000,000円 = 03 (30




高校数学 余角90 ー8の公式と補角180 ー8の公式の証明と強力な覚え方 三角比の等式の証明 Sin A B 2 Cosc 2など 受験の月




三角比の相互関係の公式4つって 証明 覚え方 応用問題6選を解説 遊ぶ数学
また、ab = a/b1 なので比の値は後項を 1 としたときの前項と言い換えることができる。後項を 100 とした前項(=100a/b)を百分率、またはパーセントという。 比例 y = kx が成り立つとき、yx の比の値 y/x と比例定数 k とは等しくなる。 ab = cd のような式を比例式という。a と d を外項、b と c を内項という。このとき、それぞれの比の値が等しいので、a/b = c/d が数学の問題では、連比は①と②の両方が出てきますので同じものだと思っていて良いです。 ただ、計算を進める上では②の形に直すと便利です。 連比を利用し式の値を求める計算問題の解き方 例題で見比例式とは12=24のように、数の比を等式で示したものです。 2つの比だけでなく、3つの比を等式で表すことも可能です。 また比例式ab=cdは、ad=bcに変形できます。 例えば12=24⇒1×4=2×2ですね。 今回は比例式の意味、問題と解き方、3つの比の計算、比例式と分数の関係について説明します。 「比」の計算、3つの数の比は下記も参考になります。 比率とは? 1




比と比の値 その2 家庭学習レシピ




高校数学無料問題集 数 第3章 図形と計量 三角比の拡張と相互関係の式 桝 ます Note
比"3 9″は両方の数を3で割れば、"1 3 ″になりますね。 よって、比"1 3″と比"3 9″は等しいことになります。 つまり、 1 3 = 3 9 といえます。 このとき、比例式の外側の数である1と9をかけると、9になります。 また、比例式の内側の数である3と3をかけると、9になります。 このよ




比例式の問題の解き方 数学fun




6azrbqy7eqexmm
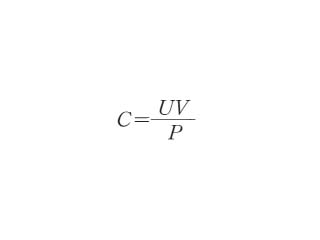



クリアランス比の公式とは コトバンク




中1数学 比と比例式 比の値 とはなんだろう Qikeru 学びを楽しくわかりやすく




比率の計算




2 の解説で 比の式で 8 1 となってるのはなんでですか Clearnote
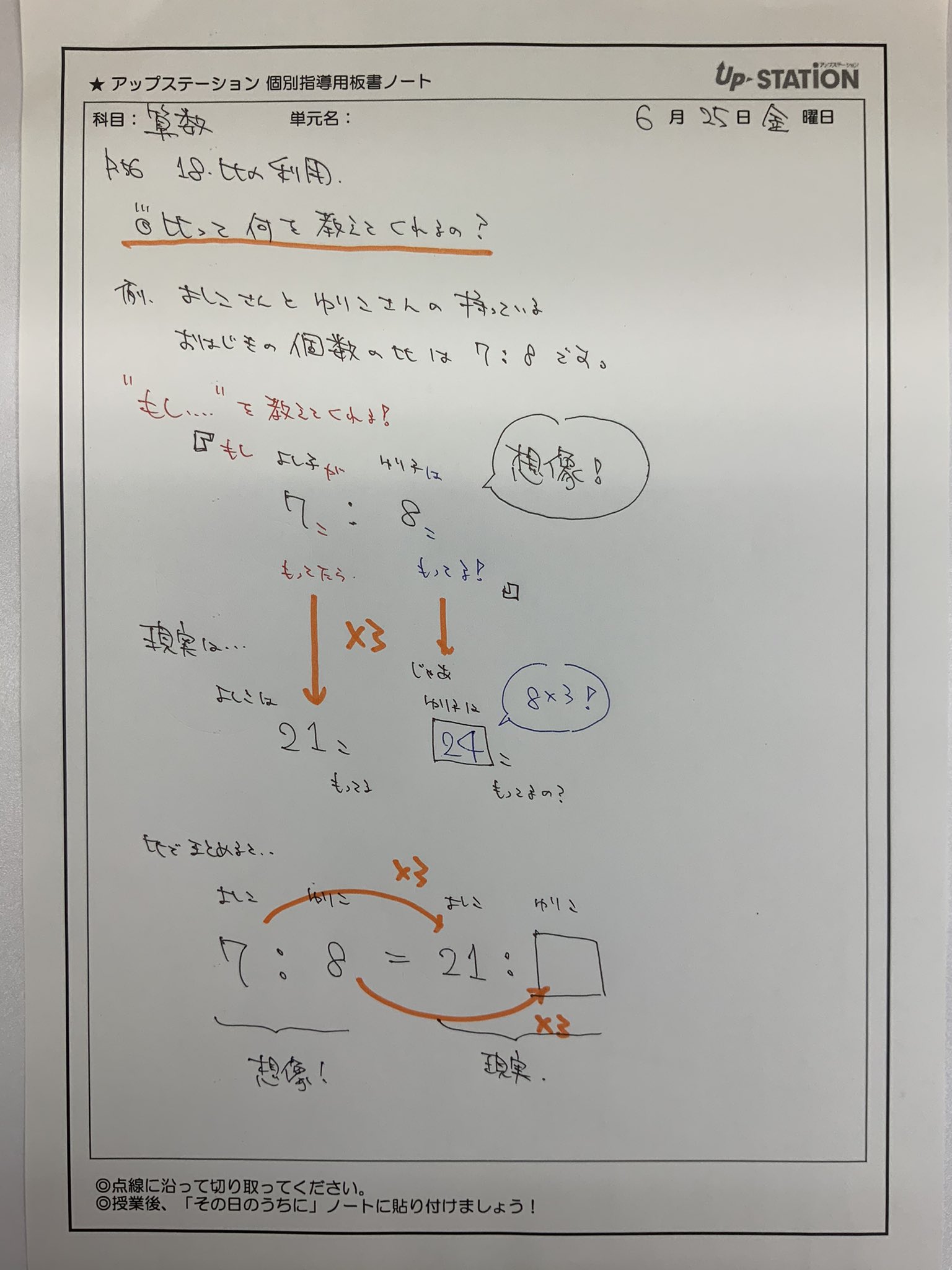



個別指導塾 アップステーション 小6算数 比の利用 比の文章題を解いているときに どんなことを考えていますか ただ闇雲に 比の式を立てて解くのではなく 問題文を読んで頭の中でイメージをもてるといいですね 個別指導 アップステーション 算数
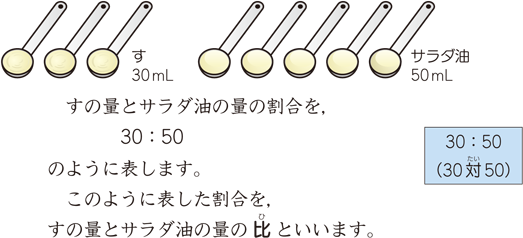



比と比の値 算数用語集




比率の計算




数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ
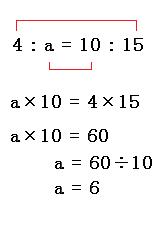



比の性質を解説 比例式や連比の解き方だってこんなに簡単
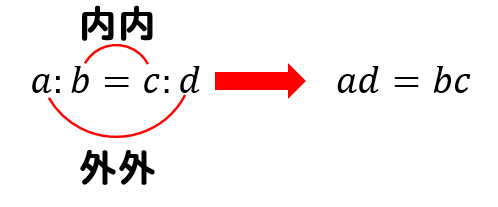



比例式の解き方は かっこがついている式の計算方法は 数スタ
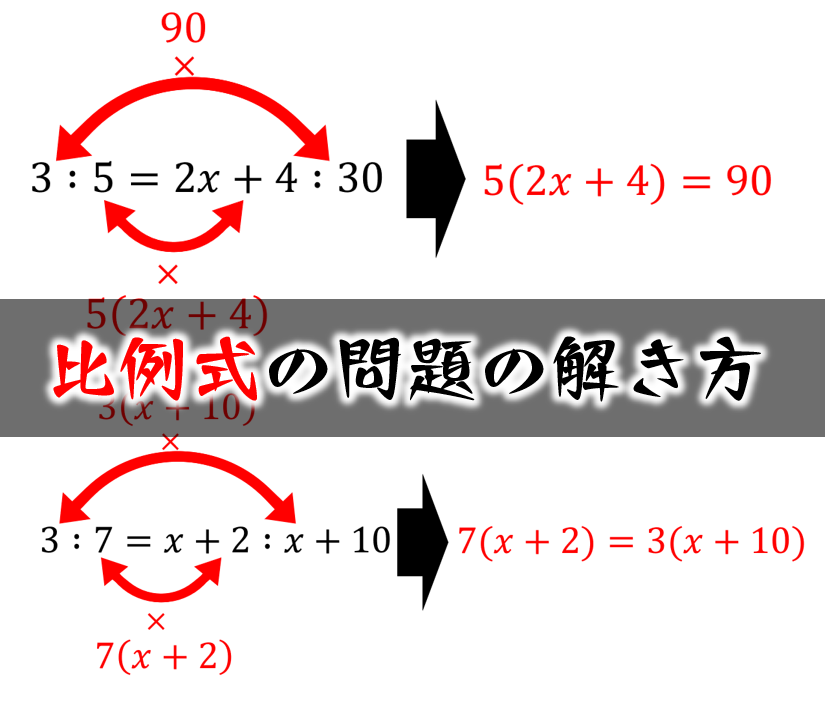



比例式の問題の解き方 数学fun




比例式の性質 3分でわかる 比例式の解き方 Qikeru 学びを楽しくわかりやすく




高校数学 数 77 三角比 公式編 Youtube



Studydoctor三角比の相互関係と計算 高校数学 Studydoctor




比の計算問題 比を簡単にする方法は小学生でもできる 中学や高校の数学の計算問題
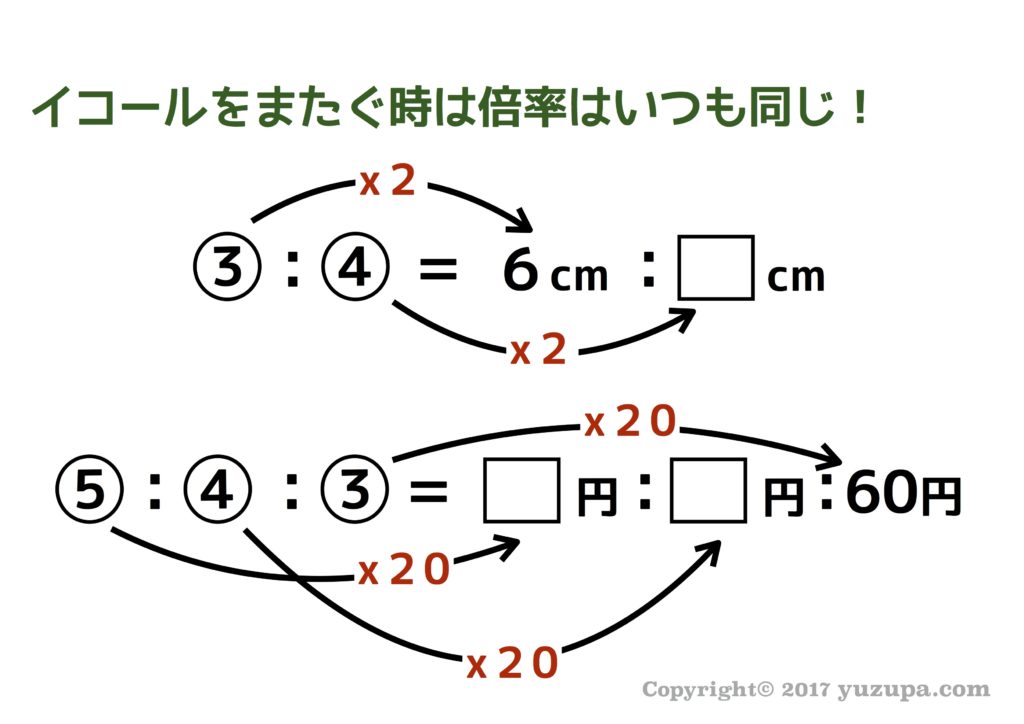



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋



6年算数比とその利用 わかる教え方1




の面積比の式についてよくわかりません 教えてください Clearnote




比と比の値についての自主学習ノート例 家庭学習レシピ
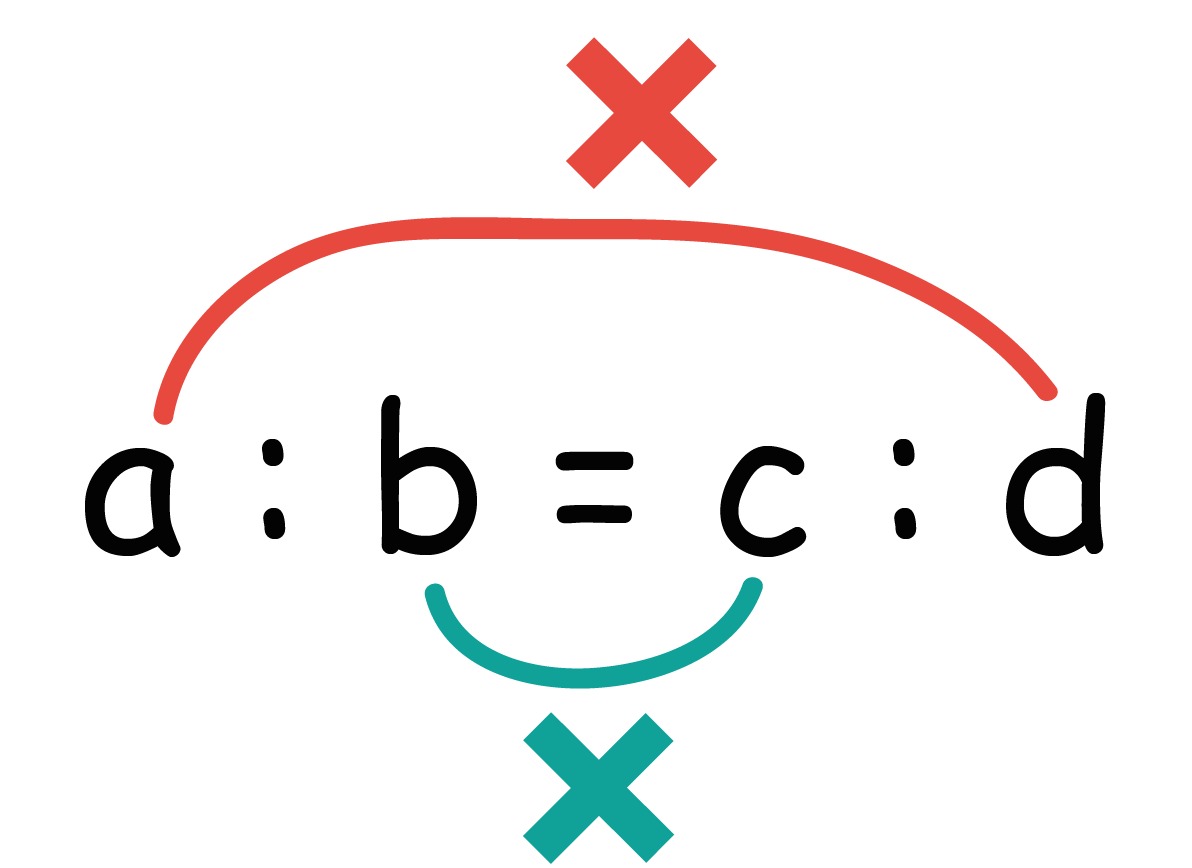



比例式の性質 3分でわかる 比例式の解き方 Qikeru 学びを楽しくわかりやすく




30 三角比の相互関係 式の値 の解き方を教えてください Clear



比の値 Youtube




計算問題に最適 コレダケ でわかる 比 の使い方 がんばれ看護学生 メディックメディア




比例式の性質 3分でわかる 比例式の解き方 Qikeru 学びを楽しくわかりやすく




比例式の性質 3分でわかる 比例式の解き方 Qikeru 学びを楽しくわかりやすく
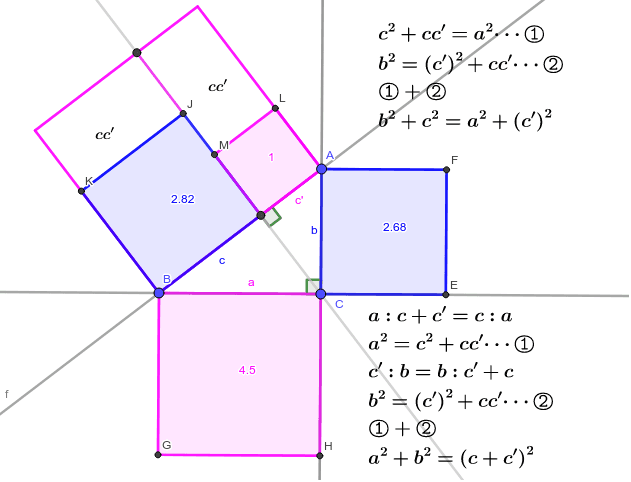



ピタゴラスの定理の拡張 その2 Geogebra




比の値と比例式 方程式 中1数学 Youtube




等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信




小6 比 比の計算 比を用いて面積を求めよう 日本語版 Youtube



6年算数比とその利用 わかる教え方1
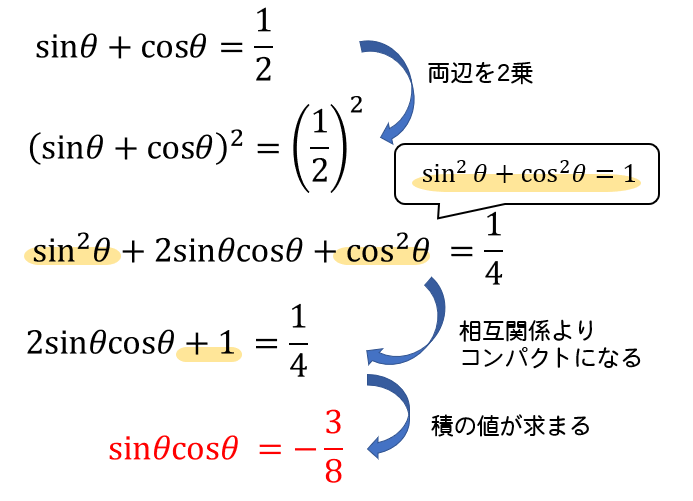



数学 三角比の式の値を求めよ 隠れた条件を見落とすな 数スタ




比と比の値についての自主学習ノート例 家庭学習レシピ




小6 算数 小6 15 比と比の値 Youtube
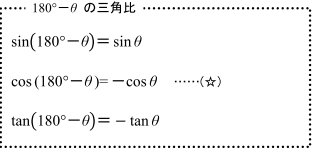



180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座
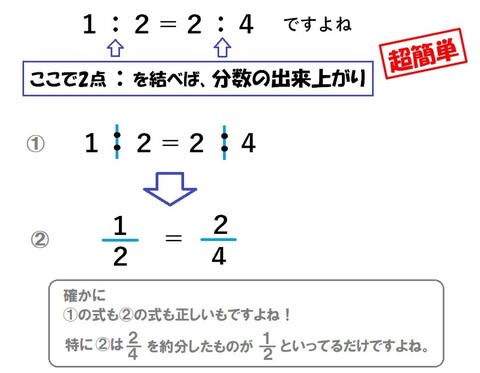



比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support




比を簡単にする Youtube




比の計算 デキる人は自然にやっている比例式の上手な計算方法 Youtube




三角比を用いた計算問題をマスターしよう スタディクラブ情報局
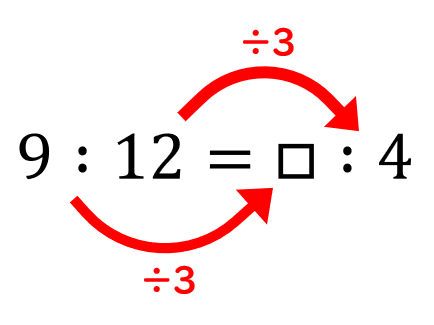



比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun
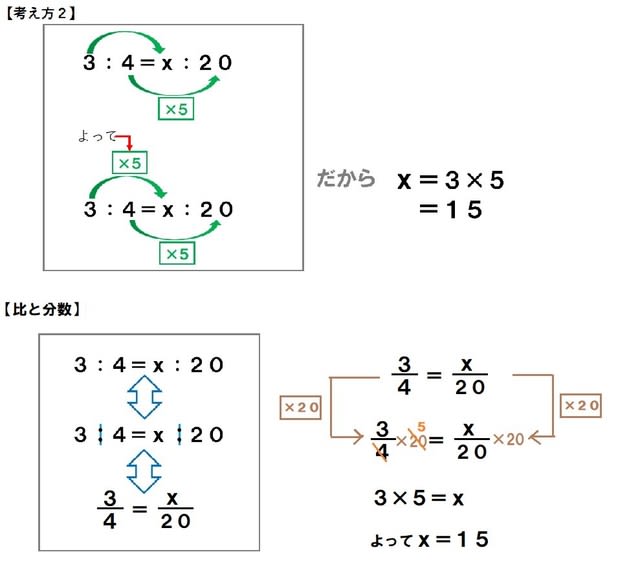



比の問題 小6 比と分数の関係 算数の教え方教えますmother S Math Happy Study Support



1




比例式 比の値 教遊者



Studydoctor三角関数の式と値 高校数学 Studydoctor
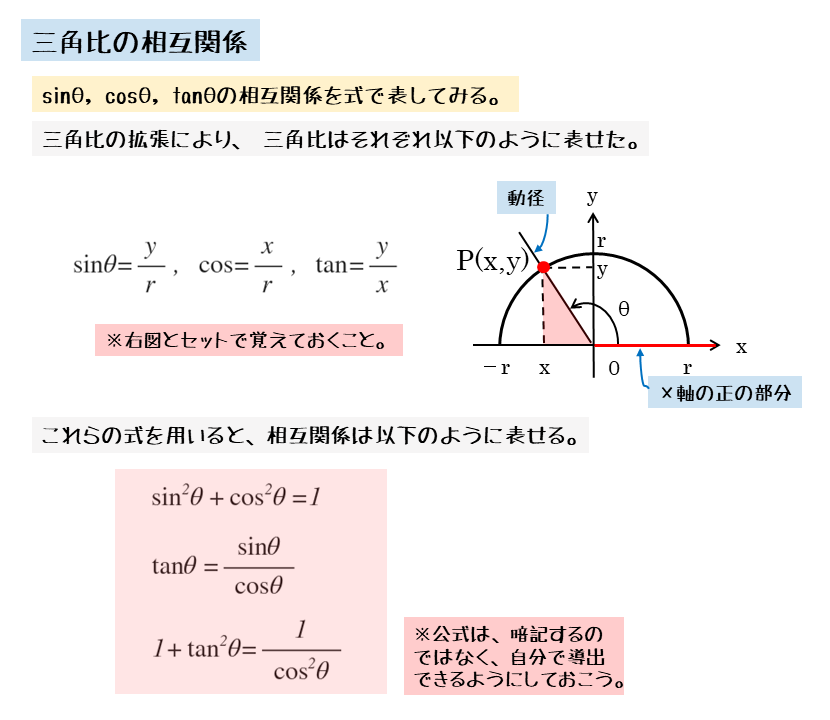



図形と計量 三角比の相互関係について その1 日々是鍛錬 ひびこれたんれん




比の計算問題を実践練習




6azrbqy7eqexmm




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



方程式の応用問題 比に関する問題 中学数学の方程式 中間 期末テスト 高校入試対策




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun
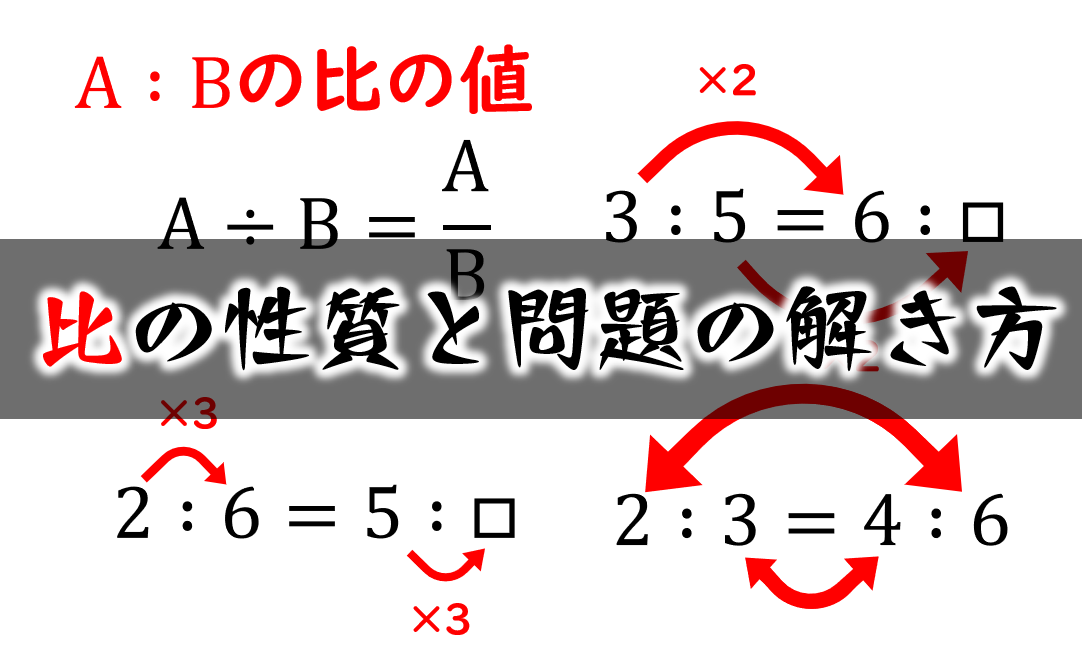



比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




簡単 画面サイズの縦横比は比例式ですぐに計算




三角比の式の値の範囲です 教えて頂きたいです Clear




比率の計算



6年算数比とその利用 わかる教え方1




数学 三角比の式と値の求め方とコツ 教科書より詳しい高校数学
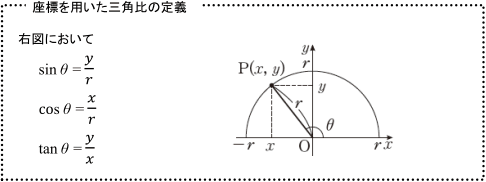



90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座



3




勉強しよう数学解答集 三角形の3頂点のベクトルの張る三角形の面積比の公式
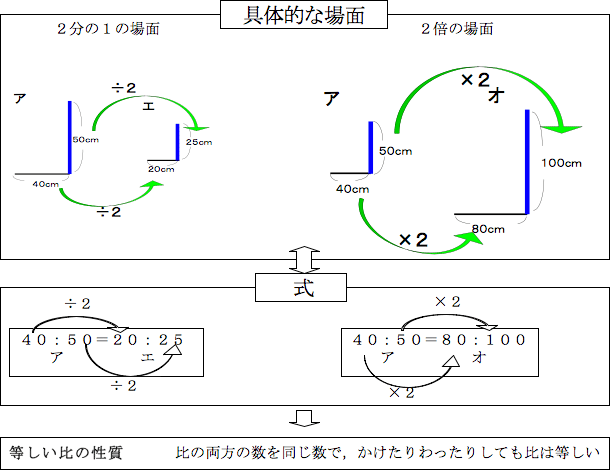



算数実践実例集 啓林館
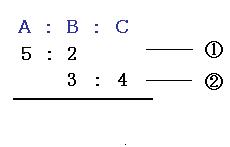



比の性質を解説 比例式や連比の解き方だってこんなに簡単



Studydoctor比の値と比例式 方程式 中1数学 Studydoctor




これらの問題なのですが 解説を読んでも全く理解出来ませんでした もっと噛み砕 Clearnote




等しい2つの比の説明 算数嫌い0 ゼロ 先生のブログ




比例式 比の値 教遊者




小6 算数 比と比の値 解説 動画 Youtube




すきるまドリル 小学6年生 算数 比と比の値 比と比の利用 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント




比の計算はこれで完璧 比の値の求め方と考え方




数列 黄金比 を計算する方法 大人が学び直す数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




高校数学 三角比の等式を満たす三角形の形状決定 受験の月
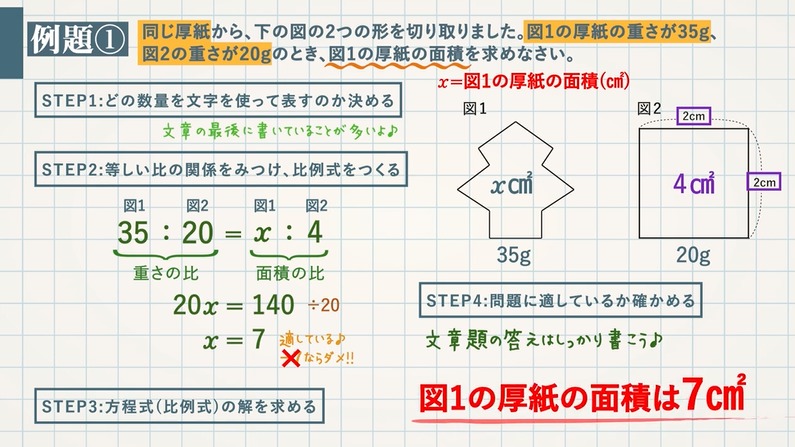



方程式の利用 比例式で解く 文章題の基本問題 教遊者



3




例題 三角比と式の値 Youtube




比と比の値についての自主学習ノート例 家庭学習レシピ
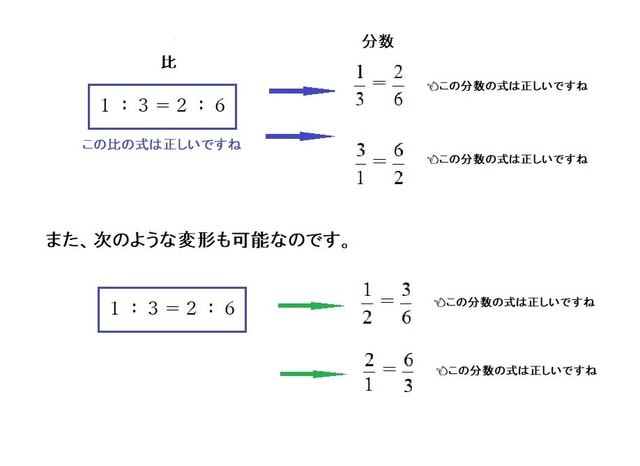



超重要 中学数学の分数準備7 比と分数 算数の教え方教えますmother S Math Happy Study Support




説明できる 比例式 内項の積 外項の積 小学生にも理解しやすい President Online プレジデントオンライン




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
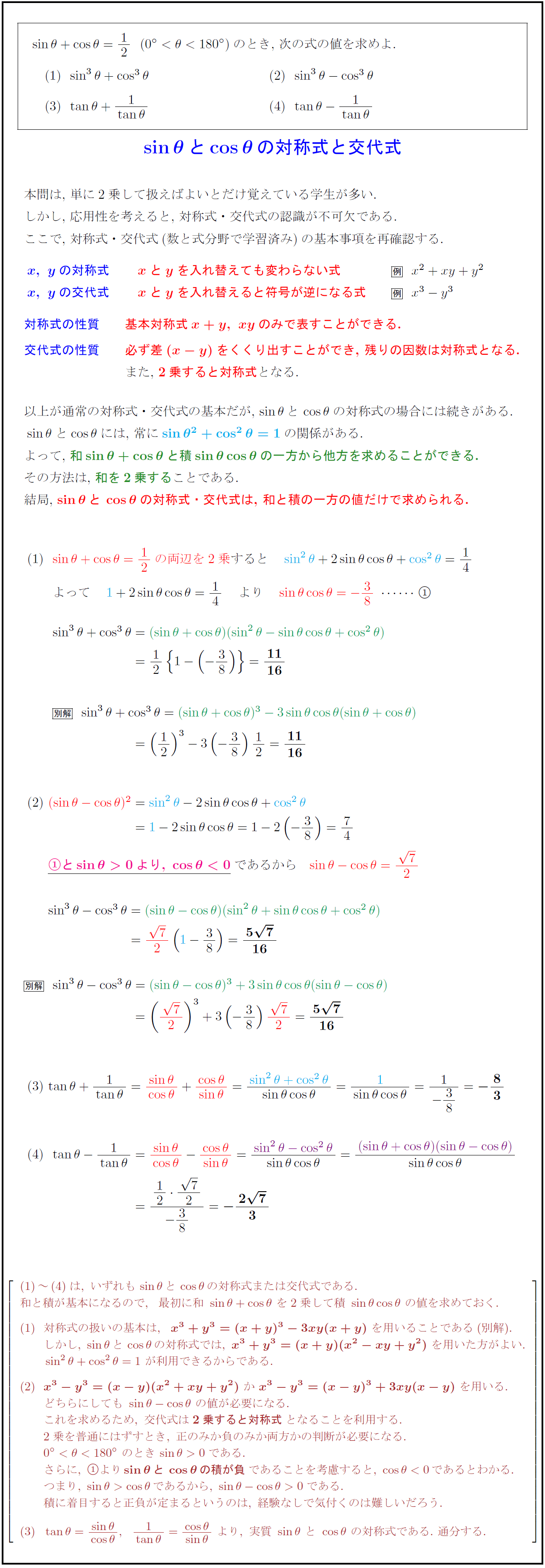



高校数学 Sin8とcos8 Tan8と1 Tan8の対称式 交代式の値 受験の月



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋




小6 算数 小6 16 比と比の値 Youtube




高校数学無料問題集 数 第3章 図形と計量 三角比の拡張と相互関係の式 桝 ます Note




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun



0 件のコメント:
コメントを投稿